Es fehlt eindeutig an deutschsprachigen Beginner-Tutorials zum Thema Neuronale Netze. Es gibt ausgesprochen gute – ich meine wirklich herausragend gut! – Tutorials zum Thema, welche man diesem hier unbedingt vorziehen sollte. Bitteschön:
- Convolutional Neural Networks for Visual Recognition by Andrej Karpathy & Fei-Fei Li
- Neural Networks Demystified by Welch Labs
- Neural Networks and Deep Learning by Michael Nielsen
- Deep Reinforcement Learning by David Silver
Doch was soll ich sagen, diese Tutorials sind umfangreich und gleich die große Kanone. Wenn man nur Spatzen haben möchte, dann hilft es vielleicht, ein einfaches Tutorial zum Einstieg zu nutzen, in dem großzügig auf Ausnahmen, Feinheiten und Randbedingungen verzichtet wird. Das versuche ich mit dem folgenden Beitrag.
Prolog
Neuronale Netze ([engl.] Neural Networks) sind schon ziemlich alt und in der Wissenschaft schon lange Thema. Seit einigen Jahren erleben sie in praktischen (medienwirksamen und leicht verständlichen) Anwendungsfällen allerdings eine unglaubliche Renissance. Ein wichtiger Grundstein war sicherlich, dass NVIDIA Ende der 2000er Jahre mit ihren CUDA Grafikkarten eine unglaubliche Rechenpower zur Verfügung stellte. Warum? Neuronale Netzwerke lernen im Grunde mit simplen Multiplikationen bzw. Faltungen, welche sich prima parallel abarbeiten lassen. Hat man mehr Prozessorkerne, hat man in überschaubarer Zeit bessere Lernkurven. Eine Quad-Core CPU stellt dabei keine relevante Anzahl Kerne dar. Das wäre, wie mit einem 50ccm Roller zu einem DTM Rennen zu kommen.
Keine Chance also, auf dem heimischen Laptop ein auch nur ansatzweise konkurrenzfähiges Neuronales Netzwerk in überschaubarer Zeit (heißt: Wochen/Monate) zu trainieren!
Was können die überhaupt so?
Am beeindruckendsten finde ich, sind derzeit folgende Neuronalen Netze (welche noch kombiniert mit so genannten Reinforcement Learning Algorithmen funktionieren und die Q-Values lernen):
- schaut auf die Pixel des Videospiels und lernt den Joystick zu bedienen: Higher Scores als Menschen in fast allen Atari Spielen der 70er Jahre: Google DeepMind’s playing Atari Breakout
- schaut auf Videobild einer Kamera und lernt, wie Motoren für Armbewegung anzusteuern sind: Kann Kleiderbügel aufhängen: End-to-End Training of Deep Visuomotor Policies
- schaut YouTube Videos und lernt, darin Situationen, Gegenstände und Tätigkeiten zu benennen: neuraltalk2 – Efficient Image Captioning [Bilder Demo – Video Demo]
- Liest übersetzte Texte und ermöglicht Echtzeit-Übersetzung von menschlicher Sprache: Skype Translator
- Schaut auf den Zeichenstil von Bildern und überträgt ihn auf jedes beliebige Foto: AI Painter – Neural Network art
- Liest sich Reden durch und imitiert Politiker: Obama-RNN – Machine Generated political speeches
- Hört sich Musik an und komponiert selbst: char-rnn composes Irish Folk music
Not bad, right? Steigen wir ein.
Begriffe

Deep Learning Wordcloud, made with https://www.jasondavies.com/wordcloud/ with words based on http://cs231n.github.io
CC-BY-SA2.0 Lizenz
Alle Begrifflichkeiten zu erläutern würde zu weit führen, aber die Wichtigsten im Überblick:
Neuron
Spricht man über ein Neuronales Netz, so ist natürlich die Frage, was ein Neuron ist. Angelehnt an die Biologie ist ein Neuron ein ‘Ding’, welches auf einen Reiz mehr oder weniger reagiert, d.h. diesen Reiz ‘durch lässt’. Je nachdem wie stark es aktiviert ist, lässt es mehr oder weniger Reiz durch.
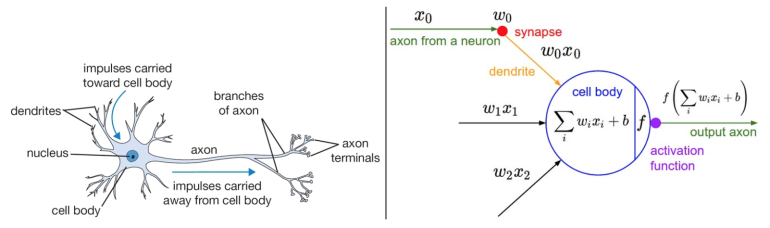
Schematische Darstellung eines Neurons aus der Biologie (links) und mathematische Darstellung für Neuronale Netze in der Computerwelt (rechts)
Source: http://cs231n.github.io/neural-networks-1/
Dabei werden Eingangswerte \(x_0, x_1, x_2, …\) mit Gewichten \(w_0, w_1, w_2, …\) multipliziert, alle Produkte summiert, noch ein Offset \(b\) hinzu addiert und alles geht als Eingang in die Aktivierungsfunktion \(f\). Resultat ist der Ausgang des Neurons, die Aktivierung. Diese kann auch wieder Mehrdimensional sein, denn wenn danach noch ein Layer folgt, so benötigt man ja für die nächste Ebene wieder Eingänge.
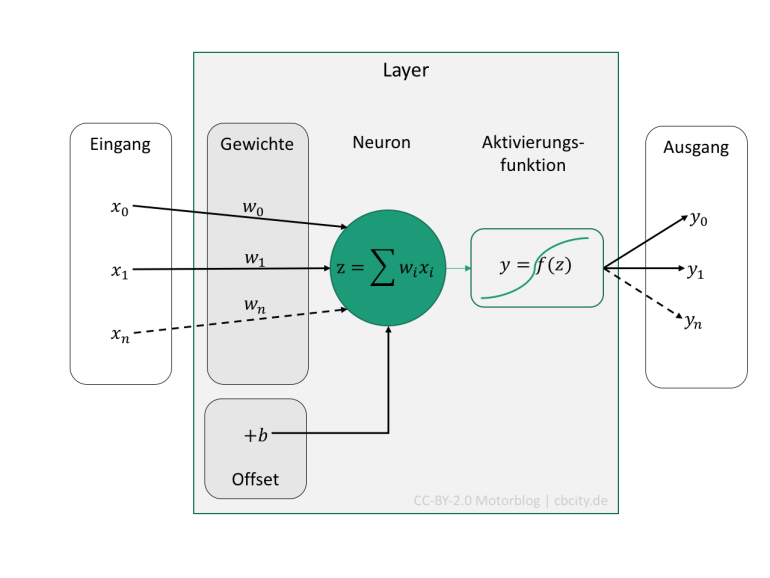
Aktivierungsfunktion / Activation Function
Spricht man nun davon, dass ein Neuron ‘aktiviert’ wird (d.h. das Netzwerk lernt), so muss man eine mathematische Funktion \(f\) hinterlegen, die diese Aktivierung modelliert. Typisch und oft genutzt ist die Sigmoid Funktion oder auch der Tangens Hyperbolicus. Großer Beliebtheit erfreut sich die ReLu (Rectifier Linear Unit) Funktion, welche eine simple \(f(x)=max(0, x)\) Funktion ist. Alle 3 sind nachfolgend dargestellt. Alle 3 sind nichtlinear, was deren Sinn ist.
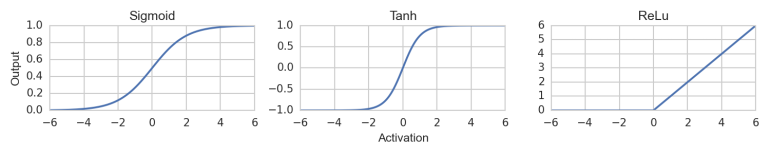
Typische Aktivierungsfunktionen: Sigmoid Funktion, Tangens Hyperbolicus und ReLu Funktion
Sie geben für einen Input (in der Abbildung beispielhaft -6…+6) je nach Aktivierung einen Output. Der funktionelle Zusammenhang ist nichtlinear. Je nachdem wie stark das Neuron aktiviert ist, gibt es ein Signal unterschiedlich stark weiter. Zu Beginn des Lernprozesses, muss jedes Neuron initialisiert werden.
Initialisierung
Wie man an den Aktivierungsfunktionen sehen kann, ist es von elementarer Bedeutung, ob ein Neuron mit 0 oder -1 oder +1 aktiviert ist. Je nach Aktivierungsfunktion lässt es ein Signal gar nicht oder teilweise oder stark durch. Zu Beginn weiß das Neuronale Netz noch gar nichts, man muss es aber initialisieren. Wenn man ein Netzwerk mit 100 Neuronen hat, sollte man 100 verschiedene Aktivierungen initialisieren.
Die Initialisierung kann im einfachsten Fall gleichverteilt erfolgen. Aber auch normalverteilt oder mit etwas ausgeklügelterer Logik. Auf keinen Fall jedoch alle mit exakt der gleichen Zahl (z.B. 0,0). Das würde dazu führen, dass jedes Neuron exakt gleich ist und beim Lernen ergäbe sich durch die Mathematik hinter dem Lernprozess, dass Fehler bzw. Korrekturen auf jedes Neuron gleich angewendet werden. Das Neuronale Netzwerk würde so nicht schlauer werden, denn es hätte ja dann nur 100 identisch dumme Neuronen.
Zielfunktion / Loss / Objective Function
Das Wichtigste am Lernen ist, dass man weiß, wann etwas richtig oder falsch war. Möchte man z.B. etwas vom Neuronalen Netz klassifziert haben (Ziffern, Buchstaben, Tiere, …), so gibt es nur ein richtig oder falsch. Eine Zielfunktion für ein Klassifizierungsproblem würde im einfachsten Fall nur die korrekt erkannten Dinge zählen. Umso mehr korrekt erkannt wurde, umso besser gelernt. Mit etwas mehr drüber nachdenken kommt man auf die Idee Softmax als Zielfunktion zu nehmen.
Es gibt aber auch Anwendungsfälle, da soll das Neuronale Netzwerk einen Wert schätzen und keine Klasse. Diese Anwendungsfälle nennt man Regressionsprobleme. Dafür ist eine andere Zielfunktion notwendig. Im einfachsten Fall berechnet man, wieviel das Netzwerk und die korrekte Funktion auseinander liegen. Diese Zielfunktionen werden L1 oder L2 Norm genannt, wobei bei letzterer der Fehler quadriert wird. In einigen Anwendungsfällen empfiehlt sich auch die Cross-Entropy als Loss Function.
Eine Zielfunktion kann aber z.B. auch ein Punktestand in einem Spiel (umso mehr, umso besser), die Anzahl an geschlagenen Figuren (umso mehr, umso besser), die erreichte Distanz (umso weiter, umso besser) oder die Entfernung zu einem Hindernis (umso dichter/weiter, umso besser). Je nach Anwendungsfall, welches das Netzwerk lösen soll.
Lernen
Kommen wir nun zum elementaren und kompliziertesten Teil: Das Lernen! Nicht nur bei Kindern ist das kompliziert, auch bei Neuronalen Netzen muss man da clever sein, um ihnen etwas beizubringen. Die Neuronen sind im ersten Schritt ja initialisiert mit zufälligen Aktivierungen. Das Netzwerk berechnet die Ausgabegröße und wird von der Zielfunktion (Loss) gnadenlos bestraft. Der Fehler den es gemacht hat, wird über so genannte Backpropagation auf die jeweiligen Neuronen zurück verteilt, die ihn verursacht haben.
Nun könnte man auf die Idee kommen, dass man die verschiedenen Neuronen einfach nach und nach einzeln durch geht und mit verschiedenen Aktivierungen (z.B. -6…6) probiert (Bruteforce), bis das Netzwerk die beste Zielfunktion ausgibt. Glückwunsch, so viel Rechenpower hat selbst Google nicht, das für halbwegs reale Anwendungsfälle durch zu spielen.
Eine etwas bessere Idee ist, zu schauen, ob der Fehler größer oder kleiner wird, wenn man die Aktivierung erhöht. Mathematisch gesehen wird die Steigung der Fehlerfunktion bestimmt. Idealer Weise gibt es eine Richtung in die man optimieren kann, sodass die Fehlerfunktion minimiert wird.
Fehlerminimierung
Diese Suche nach der idealen Aktivierung bedeutet mathematisch das Finden von Minimalwerten im Fehlerraum. Gibt es nur zwei Parameter, so kann man eine Fehlerfunktion wunderschön visualisieren. Dabei können verschiedene mathematische Suchen implementiert werden. Der Klassiker ist sicherlich die Stochastic Gradient Descent (SGD) Methode, welche numerisch einen Anstieg der Funktion bestimmt und in die abfallende Richtung optimiert. Es gibt andere Verfahren wie Nesterov Momentum, Adagrad und Adadelta oder Rmsprop. Alle haben Vor- und Nachteile sowie Parameter, welche einzustellen sind.
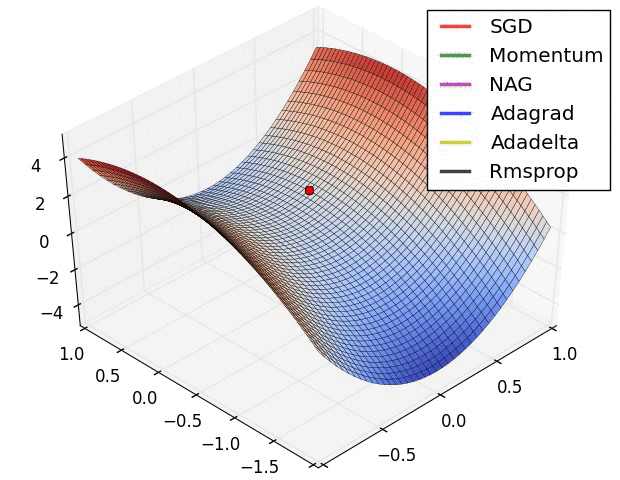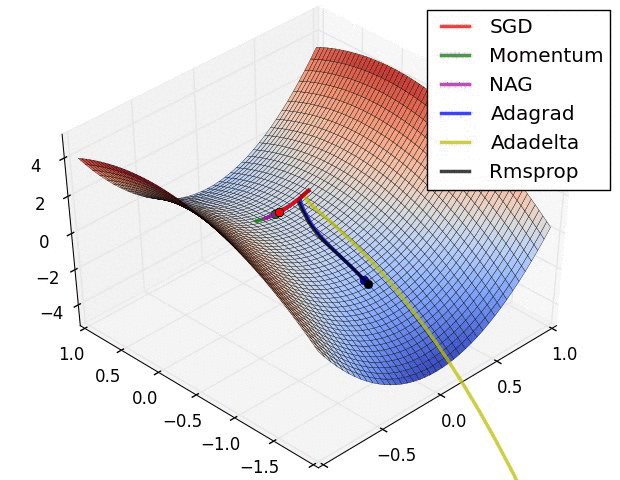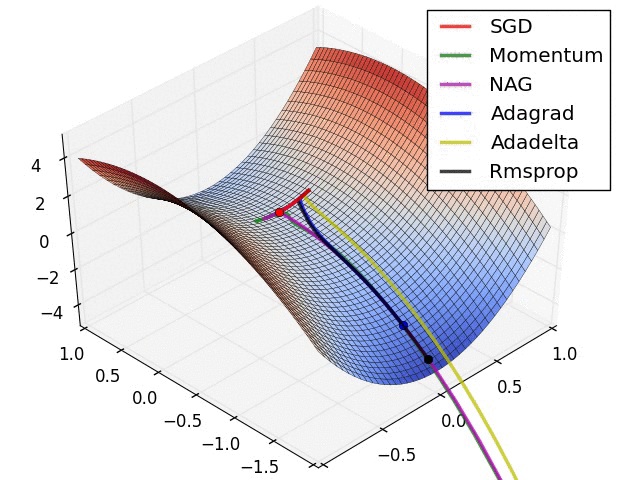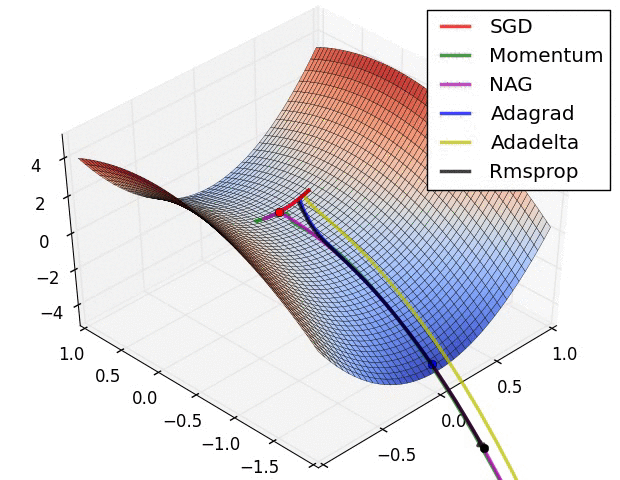
Animation credit: Alec Radford.
Backpropagation
Der Fehler \(e\), den das Netzwerk bei einer Schätzung des Ausgangswertes macht, wird zurück an das Netzwerk gegeben. Dabei wird dieser anteilig auf das Neuron verteilt, welches maßgeblich am Fehler \(e\) beteiligt war. Das mathematische Verfahren ist die Backpropagation. Man kann es sich bildlich so vorstellen:
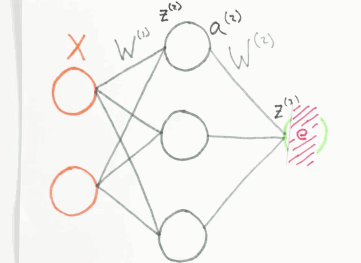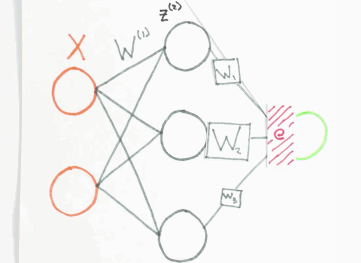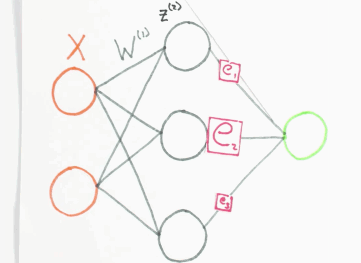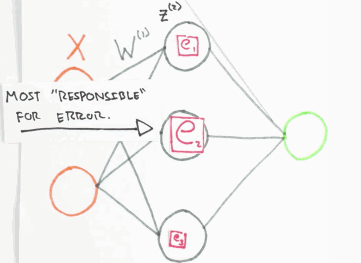
Fehler Backpropagation, orange=Input Layer, grau=Hidden Layer, grün=Output Layer, Animation by WelchLabs
Das funktioniert auch, wenn man mehr als einen Layer hat.
Layer – ab wann wird es Deep?
Ein Neuronales Netzwerk besteht aus mehreren Neuronen. Dabei gibt es verschiedene Architekturen. Es gibt aber immer einen Input- und ein Output-Layer (im GIF oberhalb orange und grün). Bei der Bezeichnung des Netzwerkes wird der Input Layer nicht mit gezählt.
Ein 3-Layer Neuronales Netzwerk hat
- Input Layer
- Hidden Layer
- Hidden Layer
- Output Layer
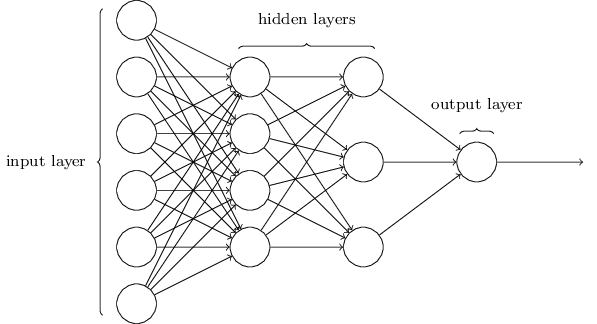
Quelle: http://neuralnetworksanddeeplearning.com/chap1.html, by Michael Nielsen
usw. Die Layer sind nacheinander (Sequentiell) angeordnet und verbunden. Ab einer gewissen Anzahl an Layern (10…20) spricht man von Deep Neural Networks.
Wenn jedes Neuron mit jedem Neuron des nächsten Layers verbunden ist, dann spricht man von ‘Fully Connected Layer’ (auch ‘Dense-Layer’). Es gibt dann so viele Gewichte \(w\), wie es Verbindungen gibt.
Soll das Netzwerk irgendwelche Informationen aus Bildern (oder Videospielen, YouTube Videos, Kamera, …) lernen, werden zur Extraktion von Features Layer eingesetzt, welche eine Faltungsoperation ausführen. Faltung (oder Englisch: Convolution, die Netzwerke heißen dann Convolutional Neuronal Network oder kurz ConvNets), ist eine relativ simple Funktion, welche in einem gleitenden Fenster das Produkt von zwei Funktionen berechnet. Es zeigt sich aber, dass dieses Vorgehen so mächtig ist, dass ein Layer damit relevante Erkennungsmerkmale für viele reale Gegenstände aus dem Bild heraus arbeitet..
Gewichte
Nun kommen wir zum eigentlichen Teil. Ein Gewicht \(w\) ist eigentlich das Elementare in einem neuronalen Netzwerk, denn es sagt, wie stark ein Neuron mit einem anderen verbunden ist. Der Ausgangswert eines Neurons, multipliziert mit dem Gewicht \(w\) und addiertem Offset \(b\), ergibt den Eingangswert für die Aktivierungsfunktion des Neurons! Mathematisch beschrieben, sieht das so aus:
\[out=f\left(\sum_iw_ix_i + b\right)\]
Wobei \(w_i\)=Gewicht, \(x_i\)=Eingangswert (bzw. Ausgangswert des Neurons des vorhergehenden Layers), \(b\)=Offset des Layers und \(f\)=Aktivierungsfunktion (z.B. Sigmoid). Der Index \(i\) bezieht sich darauf, wieviel Verbindungen auf das Neuron kommen. Besteht der Layer aus 10 Neuronen, wäre \(i=10\). Der Offset \(b\) ist ohne Index, dieser ist pro Layer für jedes Neuron konstant.
Im Code liegt die Wahrheit, hier ist also welcher, Quelle: CS231n
# forward-pass of a 3-layer neural network: f = lambda x: 1.0/(1.0 + np.exp(-x)) # activation function (use sigmoid) x = np.random.randn(3, 1) # random input vector of three numbers (3x1) h1 = f(np.dot(W1, x) + b1) # calculate first hidden layer activations (4x1) h2 = f(np.dot(W2, h1) + b2) # calculate second hidden layer activations (4x1) out = np.dot(W3, h2) + b3 # output neuron (1x1)
Im Code oberhalb sind die Variablen \(W1, W2, W3, b1, b2, b3\) das, was das Neuronale Netzwerk ‘lernen’ muss (wobei die Dimension von \(W_i\) und \(b_i\) von der Dimension der Eingangsdaten abhängt). D.h. die Backpropagation muss den Fehler so auf die \(W_i\) und \(b\) verteilen, dass der Fehler zwischen \(out\) und dem korrekten Wert minimal wird.
Die `numpy dot` Funktion bedeutet elementweise Multiplikation von Matrix-Elementen, denn was in der Formel als Summe dargestellt ist, kann natürlich effizient als elementweise Matrixmultiplikation in einem Rutsch ausgeführt werden. Es ist keine zeitaufwendige Schleife für die Summe notwendig.
Ein Neural Network ist im Prinzip eine wiederholte Matrixmultiplikation mit eingearbeiteter Aktivierungsfunktion.
Nun haben wir alles beisammen, was man benötigt, um ein Neuronales Netzwerk aufzusetzen.
Einfaches Neuronales Netzwerk mit Python und Keras
Wie im ersten Teil erwähnt, bringt es nichts auf dem heimischen Laptop ein Netzwerk aufzusetzen, was Super Mario spielen lernt. Es ist prinzipiell möglich, doch die Lernzeit ist so lang, dass bis zum Erreichen eines respektablen Erfolges viele Sommer vergehen werden.
Wir nehmen ein sehr einfaches Beispiel.
Eine beliebige Funktion approximieren mit einem Neuronalen Netzwerk
Ein Neuronales Netz ist per Definition ein universeller Approximator. Das bedeutet, dass es bereits mit einem Hidden Layer prinzipiell (und mit gewissem Fehler) jede Funktion nachahmen kann. Voraussetzung ist, dass es genügend Neuronen in dem Layer gibt und diese eine nichtlineare Aktivierungsfunktion haben.
Wir könnten den Code prinzipiell selbst in Python aufsetzen [siehe z.B. hier], doch das ist uneffizient und nicht sehr clever.
Besser ist es, eine Bibliothek zu verwenden, die das perfekt macht. Da kann man endlos durch probieren: What is the best deep learning library at the current stage for working on large data?
Theano, Lasagne, TensorFlow, Keras – Welche Bibliothek sollte ich nutzen?
Das Feld der Neuronalen Netze ist so populär, dass ca. täglich neue Bibliotheken und Wrapper für C++, Lua, Python oder Java auf Github erscheinen, welche mehr oder weniger Beta sind und mehr oder weniger Dokumentation besitzen. Auch die Big Player wie facebook oder Google veröffentlichen ihre Bibliotheken. Wer die Wahl hat, hat die Qual.
Als Anfänger sollte man darauf achten, dass man nicht erst 2 Wochen mit dem Setup für GPU und AWS Cloud zubringt, bevor man überhaupt das 1. mal anfängt rumzuspielen. Daher empfehle ich: Python > Theano > Keras!
HowTo: Funktion approximieren mit Neuronalem Netz in Python
Man kann natürlich gleich mit realen Fragestellungen beginnen, doch da lässt sich schwerlich verstehen, worum es im Kern geht. Daher als Beispiel eine gaaaaaanz einfache Sache: Es gibt eine Funktion \(f(x)\), welche dem Netzwerk nicht bekannt ist. Es soll ein neuronales Netzwerk \(g(x)\) aufgesetzt und angelernt werden, was diese Funktion approximiert.
Michael Nielsen hat dazu eine schöne Spielwiese programmiert: A visual proof that neural nets can compute any function.
Wie bekommen wir das nun mit Python, Theano und Keras aufgesetzt?
# Import Keras and Numpy Stuff we need from keras.models import Sequential from keras.layers.core import Dense, Activation from keras.optimizers import Adadelta import numpy as np f = lambda x: 0.2+0.4*x**2+0.3*x*np.sin(15*x)+0.05*np.cos(50*x) x = np.linspace(0, 1, 101) y = f(x)
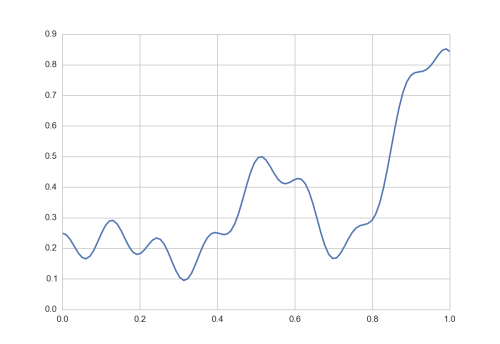
Funktion f(x), welche das Neuronale Netz lernen soll zu approximieren
Der Eingangsvektor \(x\) (kann auch eine Matrix sein, z.B. wenn mit mehreren Trainingsdaten gleichzeitig gelernt werden soll) des Neuronalen Netzwerkes besteht nun einfach aus 100 Zahlen zwischen 0…1. Der Vektor hat die Dimensionen [1, 100]:
\[x=\left[0, 0.01, 0.02, …, 1.0\right]\]
Damit die schöne Matrixstruktur und einfachen Multiplikationen funktionieren, wird der Vektor auf die Dimension [100, 1] umgestellt (also 100 lang, nicht breit). Pro Spalte in \(x\) sollte ein Trainingsdatensatz, pro Zeile ein Wert des Trainingsdatensatzes sein. Da wir nur einen Trainingsdatensatz mit 100 Werten haben, hat unser \(x\) die Form [100, 1].
X = x.reshape((-1, 1)) print(np.shape(X)) # (100, 1) print(np.shape(y)) # (100, )
Jetzt bauen wir das Neuronale Netzwerk mit Keras auf.
model = Sequential() # Sequentielles Netz, d.h. Layer nach Layer...
model.add(Dense(input_dim=1, output_dim=300, init="uniform"))
model.add(Activation("relu"))
model.add(Dense(output_dim=1, init="uniform"))
Was haben wir jetzt aufgesetzt? Ein Dense Layer ist ein Fully Connected Layer, d.h. jedes Neuron soll mit jedem des nächsten verbunden werden. Input hat die Dimension 1. Unser Inputvektor \(x\) hat die Form [100, 1]. Wie bereits beschrieben, bedeutet die Länge 100, dass wir 100 Werte haben, welche aber die Dimension 1 haben. Die Output Dimension wurde mit 300 initialisiert, das bedeutet, dass das Netzwerk 300 Neuronen bekommt im 1. Layer. Die Initialisierung soll ‘uniform’, d.h. gleichverteilt erfolgen.
Als Aktivierungsfunktion wird die ReLu Funktion hinzugefügt.
Anschließend, als Output-Layer wieder ein Fully-Connected Layer mit einer Output Dimension, d.h. das Netzwerk soll keine Klassifizierung o.ä. machen, sondern eine reale Zahl ausgeben. Diese müssen wir nun irgendwie mit dem Sollwert, d.h. der Funktion \(f(x)\) vergleichen und dem Netzwerk eine Loss-Funktion mitteilen.
model.compile(loss='mean_squared_error', optimizer=Adadelta())
In Keras wird das aufgesetzte Modell mit Loss Funktion (in dem Fall der mittlere quadratische Fehler oder auch L2 Norm genannt) und Optimizer (in dem Fall Adadelta) gleich kompiliert, d.h. wenn möglich als optimierter GPU Code im Hintergrund erzeugt.
Künstliches Neuronales Netz lernen lassen
Nun ist alles aufgesetzt und in Code gegossen. Nun kann man es lernen lassen.
model.fit(X, y, batch_size=15, nb_epoch=10000)
Das Lernen erfolgt mit jeweils 15 der 100 Werte aus dem Eingangsvektor \(x\). Die Fehlerfunktion wird 10.000x die gemachten mittleren quadratischen Fehler via Backpropagation auf die Gewichte \(w\) und \(b\) zurück verteilen. Je nach Initialisierung und Loss Funktion und Aktivierungsfunktion und gewählter Hyperparameter, lernt das Netzwerk schneller oder langsamer.
Hier kann man für einfachere Funktionen beim Lernen zusehen.
Die Loss Funktion sieht beispielsweise so aus (logarithmische y-Achse).
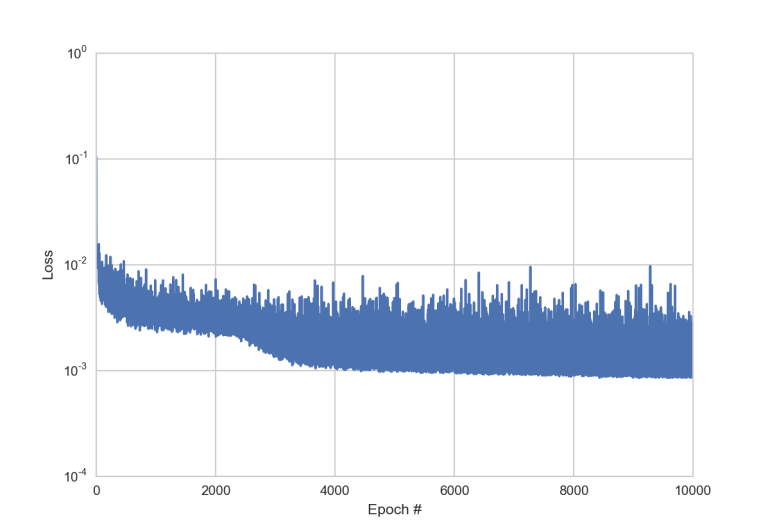
Nach 10.000 Lernvorgängen (auf einem MBP 2.9GHz, Intel Core i5 dauert das knapp 1 Minute), hat das Netzwerk die Funktion \(g(x)\) gefunden, welche \(f(x)\) approximiert.
g=model.predict(X)
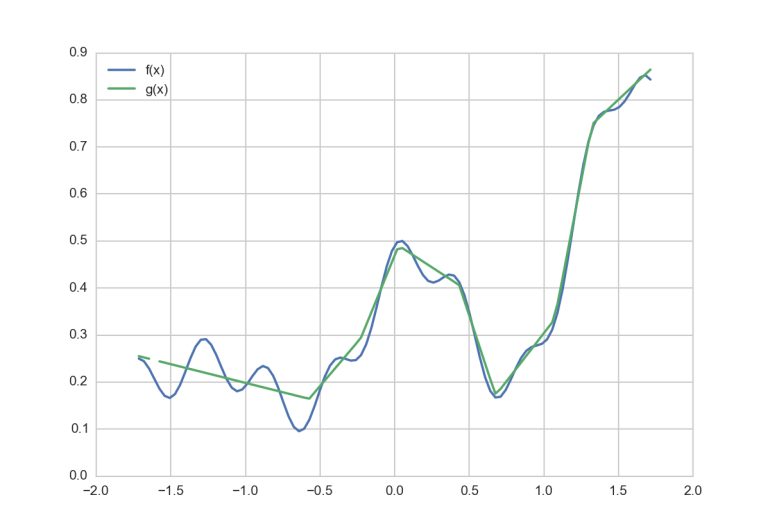
Gar nicht schlecht für 1 Minute lernen mit einem Layer mit 300 Neuronen, oder? Allerdings nicht perfekt. Vor allem der erste Teil der Funktion ist relativ schlecht approximiert. Da könnte man nun anfangen zu optimieren. Ist die Schrittweite zu groß, die Loss Funktion die richtige, die Lerndauer zu kurz, …
Bei einer Lerndauer von nur 1 Minute kann man viel rum probieren und mal schnell wieder neu anlernen. Bei einem sehr komplexen Netzwerk, mit 10 Layern und mehreren Millionen Neuronen, dauert das Lernen, selbst in Rechenzentren, einige Tage. Da ist ein gewisses KnowHow notwendig, um in die richtige Richtung zu optimieren.
Ach übrigens: Für kommerzielle Anfragen gibt es auch die Möglichkeit mich zum Thema zu konsultieren: Hire me!
— Im Teil 2 des Deep Learning Tutorials wird dieses Beispiel mit Tensorflow noch mal aufgegriffen! —
Fazit
Artificial Neural Networks sind aus der modernen Machine Learning Welt nicht mehr weg zu denken. Von der Sortierung der facebook Timeline, Siris Spracherkennung oder auch Fahrspur- und Kollisionserkennung in kamerabasierten Fahrerassistenzsystemen – überall helfen sie uns im Alltag.
Die kommende Superintelligenz?
Sofern man eine Zielfunktion aufstellen kann, ist das Lernen parallel und relativ schnell (weil der Rechner schnell prüfen kann ob es stimmt und wie groß der Fehler war) möglich. In eng eingegrenzten Szenarien (z.B. Go spielen, Atari spiele spielen, …) können sie menschliche Fähigkeiten durchaus nachahmen oder sogar besser werden als der beste Mensch in der Disziplin.
Doch ein Neuronales Netz, was Atari spielt, kann keine Sprache verstehen. Es sind keine universellen Profis. Allerdings sind die derzeit bestehenden Netzwerke auch noch wesentlich kleiner als das menschliche Gehirn. Die Biochemie im menschlichen Gehirn ist auch wesentlich komplexer als eine einfache ReLu oder Sigmoid Funktion mit ein paar Gewichten. Dennoch: Es gibt nicht wenige Gelehrte dieser Tage, die die Gefahr kommen sehen.
Ein schöner Beitrag dazu: The AI Revolution.
Künstliche Intelligenz: Gefahr für die Menschheit?
Haben wir damals in Science Fiction Filmen (Minority Report) noch über die Vorhersage von Verbrechen geschmunzelt, so ist es heute Realität.
Haben wir damals in Science Fiction Filmen (Terminator) noch über Skynet gelacht, einem Neuronalen Netz, was alle Informationen sammelt, so haben Firmen wie Google, facebook oder Geheimdienste wohl im Ansatz vergleichbare Architekturen aufgebaut.
Wann wird also der Moment gekommen sein, in dem die SciFi Vision beginnt und eine allumfassendes KI auf die Idee kommt, sich selbst zu trainieren und eigene Zielfunktionen aufzustellen? Eventuell sogar mit einem End-to-End trainierten Neuronalen Netz, welches auch gleich die Stellsignale für Elektromotoren mit lernt und physisch in Erscheinung tritt?
Hope we’re not just the biological boot loader for digital superintelligence. Unfortunately, that is increasingly probable
— Elon Musk (@elonmusk) 3. August 2014
Ein interessantes Interview zum Thema: Jürgen Schmidhuber – Intelligente Roboter werden vom Leben fasziniert sein.
Bald werden eben die klügsten Bestandteile der Zivilisation nicht mehr die Menschen sein. – Jürgen Schmidhuber





29 Comments
Wow!
Der Beitrag ist umwerfend, genau das, was ich gesucht habe! Super verständlich erklärt und eine perfekte Einleitung in das Thema Neuronale Netzwerke.
Interessant und sehr gut geschrieben. Danke dafür!
Interessant und sehr gut geschrieben. Danke dafür!
Sehr schöner Artikel, vielen Dank dafür. Besonders gut finde ich, dass mit den Anleitungen gleich losgelegt werden konnte. Ich hab schon einige paper und Artikel gelesen, dass mir die grundsätzlichen Vorgänge und Zusammenhänge irgendwie bewusst waren. Aber ein einfaches Beispiel zum einfach herumspielen hatte ich noch nicht. Oft wird ja auch gleich mit größeren Bilder-Datenbergen hantiert, was dann auch wieder Zeit brauch. Von daher “well done!”.
Jetzt noch ein paar kleine Hinweise zu Dingen die mir auffielen:
1) um Theano mit Keras (1.1.0) zu nutzen muss in der Datei ~/.keras/keras.json der Wert “backend” auf “theano” gesetzt werde. Default wird tensorflow genommen.
2) die Zeile:
x = np.linspace(0, 1, 100)
Erzeugt nicht eine Matrix die so aussieht:
x=[0,0,01,0,02,…,1,0]
Sondern eine die so aussieht:
[ 0. 0.01010101 0.02020202 0.03030303 0.04040404 0.05050505
…
0.96969697 0.97979798 0.98989899 1.]
Um die angegebene Matrix zu erhalten muss sie um ein Feld vergrößert werden, da die Null mit drin ist:
x = np.linspace(0, 1, 101)
3) Normalerweise wird die fit-Funktion so angegeben: model.fit(X, y, batch_size, nb_epoch). Also erst batch-size dann Epochenanzahl und nicht anderesherum. Was bei Dir zwar funktioniert aber beim einsetzen von Variaben für batch oder epoch zu Verwirrung führt. Getestet für sie! :)
Nun hab ich noch 2 Fragen.
F1) Könntest Du bitte mal erklären was Epochen sind? Ich bin mir nicht sicher es verstanden zu haben und konnte noch keine direkte Erklärung finden. Ich vermute, es ist einfach ein Lern-Durchgang dessen im Output irgendwie am Input weiter verwendet wird.
F2) Ich hab den Algorithmus 300k Mal durchlaufen lassen (17Min, Core i5 Laptop) und das Ergebiss war wie zu erwarten deutlich besser als bei den 10k Durchläufen. Die “Intelligenz” des Netzes ist ja nun in den Gewichten der 300 Neuronen gespeichert. Lässt diese sich da nun wieder herausholen und abspeichern? Vielleicht auch als Matrix für die Anfangswerte um immer wieder “weiter” zu lernen? Und lässt sich aus der Matrix wieder eine Formel rekonstruieren?
Danke und Grüße
Rob
Hi Rob, vielen Dank für’s Nachbauen und Review! Habe deine Hinweise eingearbeitet, danke.
Zu deinen Fragen:
F1: Epochen sind Wiederholungen. Das Gradientenabstiegsverfahren “erlaubt” ja nur relativ kleine Korrekturen (Learning Rate), weshalb man von random Initialisierung bis zum guten Ergebnis eben einfach sehr oft die kleinen Korrekturen auf die Gewichte anwenden muss. Allgemein und ohne Anspruch auf Allgemeingültigkeit gilt: Sehr kleine Learning Rate und viele Epochen ergeben (nach sehr langer Lernzeit) bessere Ergebnisse. Das Thema ist aber ein eigenes Forschungsfeld und da gibt es seeehr viel mehr zu wissen.
F2: Ja, das geht mit Keras einfach mit `model.save` (siehe Doku).
Toller Artikel!
Ich habe eine (wahrscheinlich dumme) Frage: Wenn man ein Outputneuron hat (z.B. bei einer AND Funktion), welchen Sinn macht dann softmax? Es kommt doch immer 1 raus … oder?
Wunderbar erklärt, sehr vertändlich sogar für Neulinge wie mich.
Hallo, ich bin Anfänger in Sachen neuronale Netzwerke. Ich hätte da eine grundsätzliche Frage zum Thema Fehlerberechung und entsprechender Modifikation der Stärke des jeweiligen Gewichtes. Dies wird ja auch in diesem Blog erklärt. Warum muss man sich eigentlich den Fehler berechnen und schrittweise an die richtige Gewichtsstärke annähern? Man könnte doch die richtige Stärke des Gewichtes viel einfacher berechnen mittels einer simplen Quotientenbildung wie beim Dreisatz, d.h. z.B. Gewicht(aktuell)/Gewicht(gewünscht) = LadungNeuron(aktuell)/LadungNeuron(gewünscht) => Gewicht(gewünscht) = Gewicht(aktuell) * (Ladung(gewünscht)/Ladung(aktuell)). Warum muss man sich umständlich mittels z.B. einer Quadrat-Fehlerfunktion schrittweise annähern? Offensichtlich hab ich da einen Denkfehler, oder hängt es damit zusammen, daß ja mehrere Muster gelernt werden müssen und daher die von mir vorgeschlagene Berechnung die anderen Muster bzw. erlernten Gewichte löschen würde? Vielen Dank im voraus für eine Erklärung! T.P.
Thanks for this great share. This site is a fantastic resource. Keep up the great work here at Sprint Connection! Many thanks.
pet portraits oil painting
Sun Cellular
Smart Communications
Smart Communications
Smart Communications
Sun Cellular
Sun Cellular
Smart Communications
Smart Communications
Globe Telecom
Sun Cellular
Globe Telecom
Smart Communications
Sun Cellular
Globe Telecom
Globe Telecom
Smart Communications
Smart Communications