Faustformel für Reaktions- und Bremsweg

In Fahrschulen werden gern ‘nur’ die Faustformeln für den Reaktions- und Bremsweg gelehrt. Wie kommen diese zustande?

Anhalteweg

Dieser setzt sich zusammen aus dem

• Reaktionsweg (der Weg, den man zurücklegt vom Erkennen bis zum Bremsbeginn)
• Bremsweg (der Weg, den man zurücklegt vom Bremsbeginn bis zum Stillstand)

Der Anhalteweg ist also maßgeblich abhängig von der Geschwindigkeit, Reaktionszeit und erreichbaren Verzögerung (Reifen/Straße Komination, Reibwert, Bremse, …).

Faustformel für Reaktionsweg

Während man auf das Hindernis reagiert, fährt das Auto mit konstanter Geschwindigkeit weiter. Wir nehmen \(v=100\frac{km}{h}\) an. Der Reaktionsweg ist abhängig von dieser Geschwindigkeit und der Reaktionszeit.

\[s_\text{R}=v \cdot t\]

Wobei die Faustformel von \(t=1{,}1s\) ausgeht. Es ergibt sich mit konkreten Zahlen und Beachtung der Einheiten:

\[s_\text{R}=\frac{100}{3{,}6}\frac{m}{s} \cdot 1{,}1s = 30{,}55m\]

Die Faustformel für Fahrschüler ist eine Größengleichung, d.h. es wird \(km/h\) eingesetzt aber \(m\) als Ergebnis zurück gegeben.

\[s_\text{R}= \frac{v}{10} \cdot 3 = \frac{100 \text{km/h}}{10} \cdot 3 = 30m \]

Ist die Reaktionszeit länger als 1,1s, ist der Reaktionsweg natürlich länger, aber die Faustformel geht immer von 1,1s aus, bis die Bremsung begonnen wird. Wer auf’s Smartphone schaut oder am Navi die Zieladresse eintippt, wird die Sekunde wohl nicht halten können.

Faustformel für Bremsweg

Der Bremsvorgang ist nun keine Bewegung mit konstanter Geschwindigkeit mehr. Hier wird natürlich Geschwindigkeit abgebaut. Daher ist die Formel zur Berechnung des Weges bei konstanter Verzögerung etwas komplizierter. Es wird angenommen, dass von einer Anfangsgeschwindigkeit bis zum Stillstand abgebremst wird.

Herleitung der Faustformel für den Bremsweg (Fahrschule)

Allgemein ist die Beschleunigung \(a=\frac{\Delta v}{\Delta t}\), also Geschwindigkeitsänderung pro Zeit. Umgestellt nach der Anhaltezeit ergibt sich

\[t=\frac{v}{a}\]

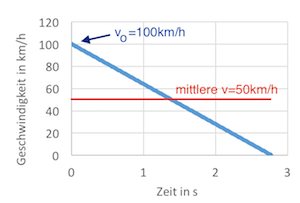
Wir interessieren uns aber nicht für die Zeit die es dauert, bis das Fahrzeug angehalten hat, sondern für den Weg. Hier müssen wir nun einen kleinen Trick anwenden, damit es einfach bleibt. Da die Geschwindigkeit von der Anfangsgeschwindigkeit \(v_0\) auf \(0 \frac{km}{h}\) reduziert wird, kann die Annahme getroffen werden, dass über die gesamte Dauer der Abbremsung die mittlere Geschwindigkeit der Hälfte der Anfangsgeschwindigkeit \(v_0\) entspricht: \(v=\frac{v_0}{2}\) (siehe Abbildung).

Nun kann die bekannte Gleichung \(v=\frac{s}{t}\) genutzt (eigentlich ja nur gültig für gleichmäßige Bewegungen) und umgestellt werden zu \(t=\frac{s}{v_0/2}\).

Das Ersetzen der Zeit in der Formel der Beschleunigung ergibt folgende Formel für den Bremsweg:

\[s_\text{B}=\frac{v_0^2}{2a}\]

Die Faustformel im Fahrschulwesen lautet als Größengleichung, d.h. ohne das Einheiten umgerechnet werden müssen:

\[s_\text{B}=\frac{v}{10}\cdot \frac{v}{10}\]

Ein Bremsweg aus 100km/h ergibt also

\[s_\text{B}=\frac{100\frac{km}{h}}{10}\cdot \frac{100\frac{km}{h}}{10}=100m\]

Wie kommt man nun darauf \(s_\text{B}=\frac{v^2}{2a}\) zu \(s_\text{B}= \frac{v}{10} \cdot \frac{v}{10}\) zu vereinfachen? Die Größengleichung berücksichtigt die Umrechnung von km/h in m/s (zum Quadrat) und die 2 im Nenner. Dabei wird in der Faustformel für Fahrschulen eine mittlere Verzögerung von \(a=3{,}86\frac{m}{s^2}\) angenommen, damit dabei rund 100 heraus kommt: \(3{,}6^2 \cdot 2 \cdot 3{,}86 \approx 100\). Und diese Hundert kann man schön in \(10 \cdot 10\) schreiben. Fertig ist die Faustformel \(\frac{v}{10}\cdot \frac{v}{10}\).

Aus \(v=100\frac{km}{h}\) ergibt sich mit der korrekten Formel ebenfalls ein Bremsweg von 100m:

\[s_\text{B}=\frac{\left(100\frac{km}{h}\right)^2}{2\cdot 3{,}86\frac{m}{s^2}}=\frac{\left(27{,}7\frac{m}{s}\right)^2}{2\cdot 3{,}86\frac{m}{s^2}}=100m\]

Kann der Bremsweg auch kürzer sein?

Ja, natürlich. Die in der Faustformel angenommene Verzögerung von \(a=3{,}86\frac{m}{s^2}\) ist keine Vollverzögerung. Auf trockener Fahrbahn kann ein normaler PKW \(a=7…8\frac{m}{s^2}\) Verzögerung erreichen. Hier ein Verzögerungsverlauf bei Vollbremsung mit einem Volkswagen T5.

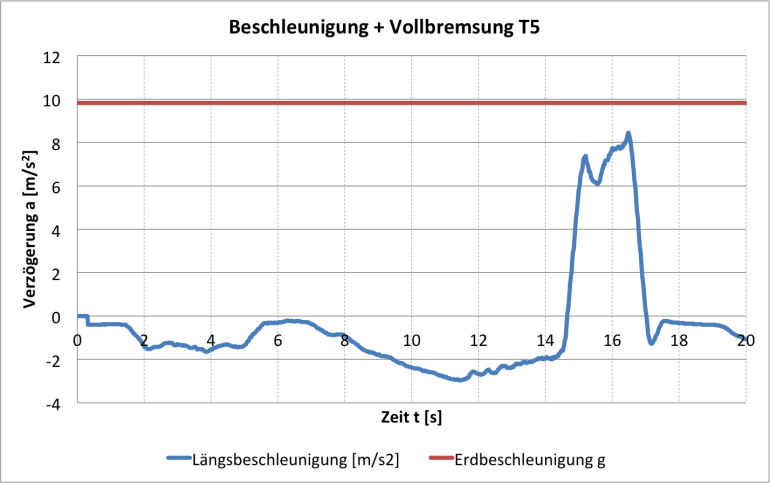
Bei guter Reifen/Straßen-Kombination, Nutzung von Bremsassistenten und günstiger Schwerpunktlage können auch Verzögerungen von reichlich \(a=11\frac{m}{s^2}\) erreicht werden.

Bremsweg-Tests in Automobilmagazinen ergeben für Sportwagen (hier: Porsche 911 GT3) Bremswege von \(s=31{,}5m\) aus 100km/h, was gleichbedeutend mit einer mittleren Verzögerung von

\[a=\frac{v^2}{2s}=\frac{\left(100\frac{km}{h}\right)^2}{2\cdot 35m}=12{,}25\frac{m}{s^2}\]

Dies entspricht einem Reibwert zwischen Reifen und Straße von \(\mu=\frac{12{,}25\frac{m}{s^2}}{9{,}81\frac{m}{s^2}}=1{,}25\). Ganz schön großer Kamm’scher Kreis!

---

Titelbild “Porsche Felge” unter CC-BY-SA2.0 Lizenz von Alex Schmitt von flickr.com