Zweiräder müssen sich bei Geschwindigkeiten über 0km/h neigen, um eine Kurve durchfahren zu können. Das liegt daran, dass das Fahrzeug die auftretenden Fliehkräfte mit entsprechender Gewichtskraft ausgleichen müssen. Mitunter sieht das recht spektakulär aus, wie am Beispiel Casey Stoner eindrucksvoll zu sehen.
Doch welcher Winkel stellt sich denn ein und wie weit kann man sich überhaupt in die Kurve legen?
Motorrad ohne Kurve
Steht ein Motorrad exakt senkrecht, so würde es theoretisch auch nicht umkippen. Kleinste Kippwinkel führen allerdings dazu, dass es in der Realität immer irgendwann umkippt. Doch bei völlig exakter 0° Lage, würde es stehen und die Gewichtskraft zeigt exakt vom Schwerpunkt auf den Radaufstandspunkt.
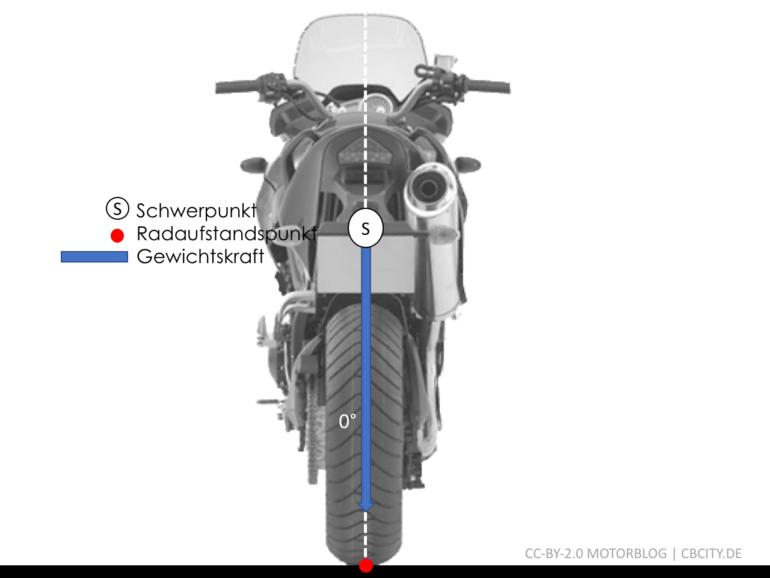
Motorrad ohne Schräglage
Die Gewichtskraft ergibt sich durch Masse und Erdbeschleunigung \(F_{G}=m \cdot g\).
Sobald eine Kurve gefahren wird, ändert sich die Querdynamik allerdings.
Schräglage abhängig von Kurvengeschwindigkeit und -radius
Anmerkung: Alle Aussagen in diesem Beitrag sind vereinfacht und gelten genau genommen nur für unendlich schmale Reifen!
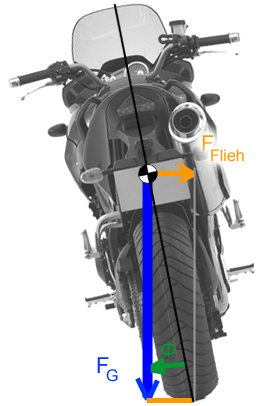 Bei Kurvenfahrten, ergeben sich Fliehkräfte, die am Schwerpunkt in Richtung Kurvenäußeres ziehen.
Bei Kurvenfahrten, ergeben sich Fliehkräfte, die am Schwerpunkt in Richtung Kurvenäußeres ziehen.
Die Fliehkraft, welcher mit der Schräglage entgegen gewirkt werden muss, ist abhängig von dem Kurvenradius \(R\), der Masse \(m\) und der Geschwindigkeit \(v\), mit welcher man durch die Kurve fährt.
\[F_\text{Flieh}=m \cdot \frac{v^2}{R}\]
Die Fliehkraft zieht das Motorrad nach außen. Dabei ist anzumerken, dass die Geschwindigkeit quadratisch in die Fliehkraft eingeht. Es macht durchaus einen Unterschied, ob man die Landstraße mit 100km/h oder 120km/h befährt, denn die aufzubringenden Kräfte sind überproportional höher.
Ein Motorrad benötigt eine Kraft, welche bei Kurvenfahrt nach innen ‘zieht’, da es sonst in Richtung der Fliehkraft umkippt.
Warum kippt ein Motorrad trotz Schräglage in der Kurve nicht um?
Die Masse des Motorrades (Gewichtskraft) möchte es umkippen lassen, sobald es mit einem Winkel \(\phi\) geneigt wird. Dabei zieht der Sinus-Anteil der Gewichtskraft das Motorrad nach innen und wirkt der Fliehkraft genau entgegen.
\[F_\text{Kipp}=m \cdot g \cdot \sin(\phi)\]
es wirkt dann \(F_\text{Kipp}=F_\text{Flieh}\) und die Kräfte sind ausgeglichen.
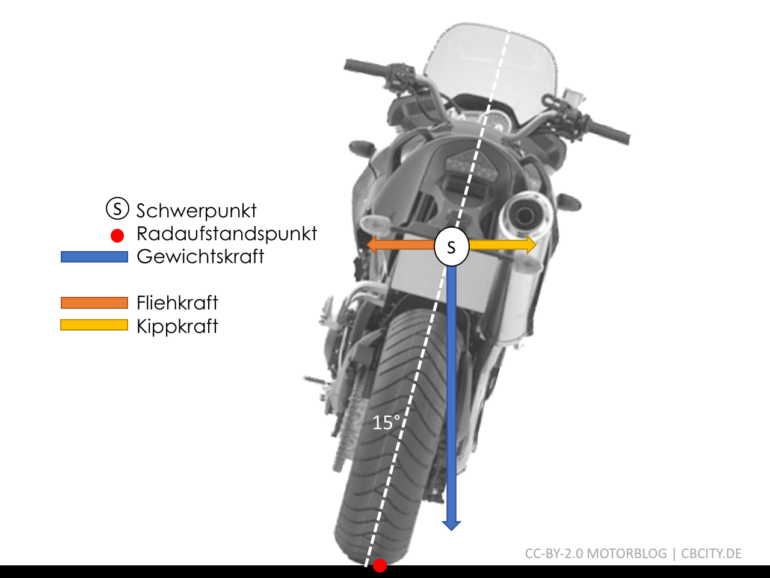
Den richtigen Winkel für eine Geschwindigkeit wählen läuft mehr oder weniger intuitiv, der Mensch “lernt Motorrad fahren”.
Motorrad Schräglage und tatsächliche Schräglage
Vereinfacht wird oftmals angenommen, dass der Reifen unendlich dünn ist, doch sollte man sich die tatsächlichen Gegebenheiten mal ansehen.
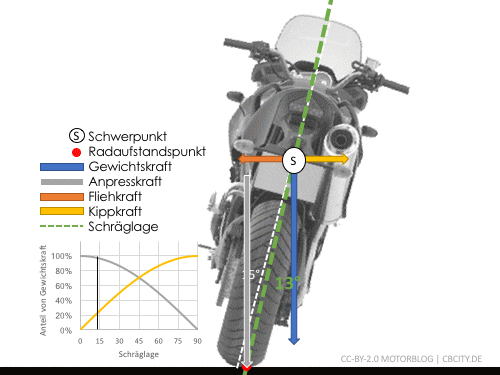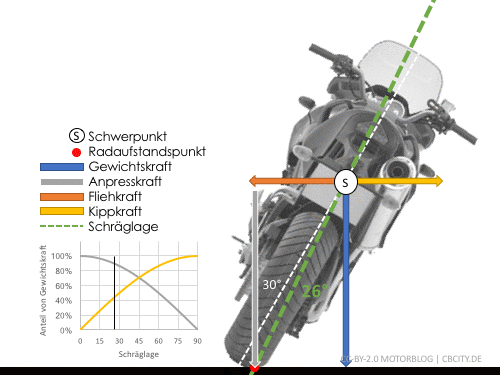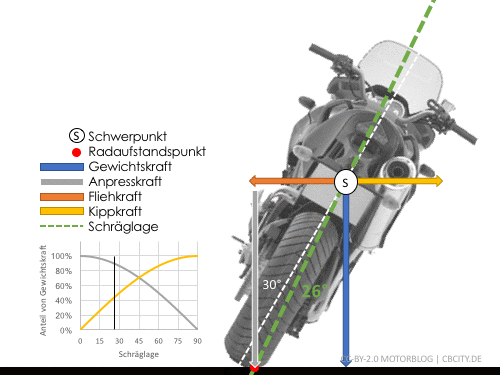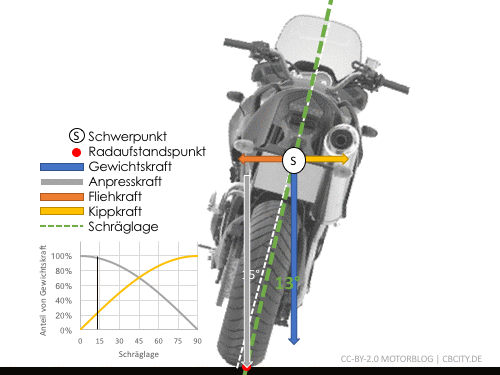
Es ist zu unterscheiden zwischen dem Neigungswinkel des Motorrades und dem tatsächlichen Neigungswinkel, welcher sich zwischen Radaufstandspunkt und Schwerpunkt ergibt (grüne Linie). Diese Neigung ist entscheidend für die Fahrphysik. Wie man sieht ist diese von Reifenbreite und Schwerpunkthöhe abhängig, was aber in vielen Aussagen und Formeln vernachlässigt wird.
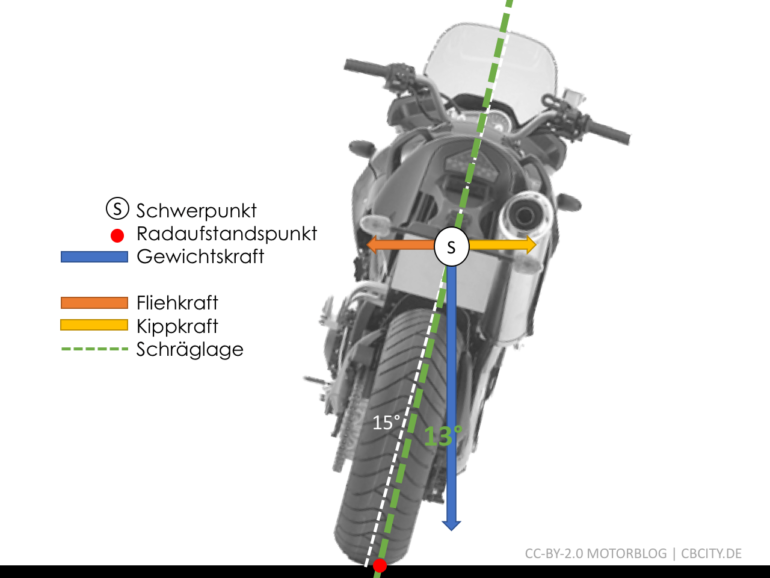
Motorrad in Schräglage mit am Schwerpunkt angreifenden Kräften und resultierender tatsächlicher Schräglage (grün)
Reifen erzeugen Seitenführungskraft
Die Reifen erzeugen eine zum Kurvenmittelpunkt zeigende Kraft, welche der Fliehkraft exakt entgegen wirkt. Die Kraft die Senkrecht nach unten auf die Reifen wirkt ist die Anpresskraft (auch Normalkraft genannt). Steht das Motorrad senkrecht wirkt die gesamte Gewichtskraft als Anpresskraft. Sobald es jedoch mit einem Neigungswinkel \(\phi\) in Schräglage gerät, wirkt nur noch der Cosinus-Anteil der Gewichtskraft als Anpresskraft: \(F_\text{Anpress}=m \cdot g \cdot \cos(\phi)\).
Der Reifen muss bei zunehmender Schräglage immer mehr Seitenführungskraft bei immer weniger Anpresskraft aufbringen. Dabei nimmt die Anpresskraft mit dem Cosinus ab, die notwendige Seitenführungskraft aber mit dem Sinus zu. Das Verhältnis von Sinus und Cosinus ist der Tangens \(\frac{\sin(\phi)}{\cos(\phi)}=\tan(\phi)\).
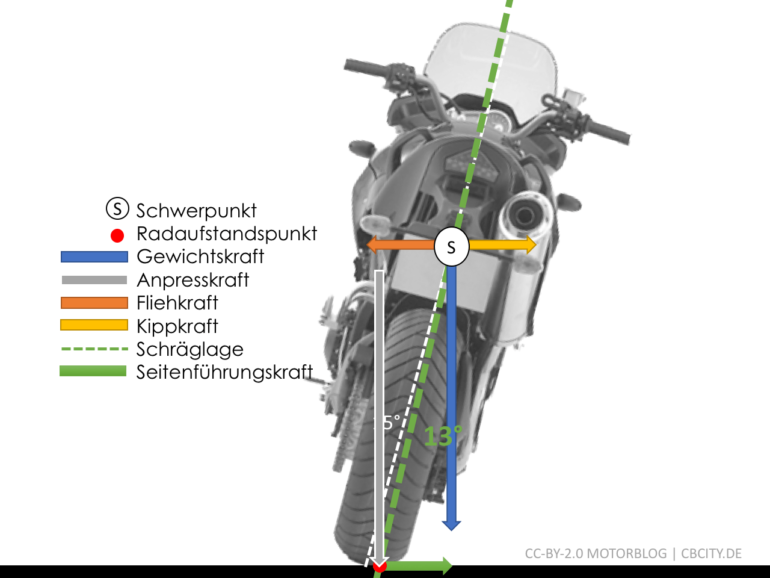
Kräfte am Rad während einer Kurvenfahrt: Der Reifen muss aus der Anpresskraft (grau) so viel Seitenführungskraft (grün) erzeugen, wie die Fliehkraft (orange) verlangt
Diese beiden Kräfte (orange und grün im Bild) müssen sich bei Kurvenfahrt nun ausgleichen: \(F_\text{Flieh}=F_\text{Seiten}\)
\[m\cdot\frac{v^2}{R}=m\cdot g \cdot \tan(\phi)\]
Der Tangens des Schräglagenwinkels ist in diesem Fall nichts weiter als der Reibwert \(\tan(\phi) = \mu\).
Schräglagenwinkel Motorrad
Der Schräglagenwinkel, welche sich bei Kurvenfahrt einstellt (und unabhängig von der Masse ist), ist im idealisierten Fall (ohne Reifenbreite und Schwerpunkthöhe):
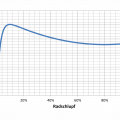
\[\phi = \arctan \left( \frac{v^2}{R \cdot g} \right)\]
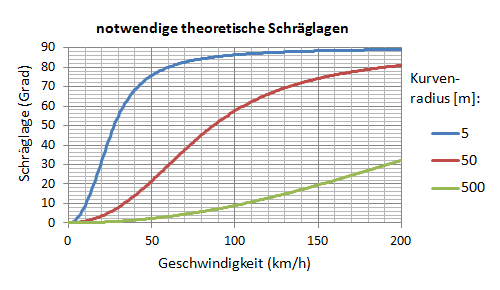
Auf den ersten Blick merkwürdig erscheint, dass es ab einer bestimmten Schräglage kaum noch notwendig ist, sich weiter in die Kurve zu legen, obwohl die Geschwindigkeit ansteigt. Warum es diesen asymptotischen Verlauf bei 90° gibt, wird im nächsten Abschnitt geklärt.
Maximale Kurvengeschwindigkeit
Interessant ist ja jetzt die Frage, wie hoch die maximale Kurvengeschwindigkeit sein darf, mit welcher man gerade noch so durch die Kurve kommt. Dazu muss ein Blick auf die Kontaktfläche zwischen Reifen & Fahrbahn geworfen werden. Die Kraft, welche vom Reifen aufgebracht werden kann, wird durch den Haftreibungskoeffizienten µ definiert. Er gibt an, wie viel Seitenführungskraft pro Anpresskraft aufgebracht werden kann.
\[\phi_\text{max}=\arctan(\mu)\]
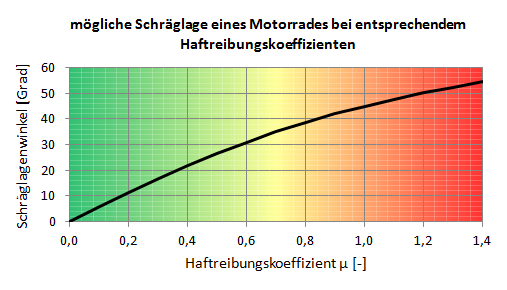
Da nun der nötige Schräglagenwinkel und die Geschwindigkeit zusammen gehören, kann man auf eine Höchstgeschwindigkeit in Abhängigkeit des Haftreibungskoeffizienten µ schließen.
\[v_\text{max}=\sqrt{\mu \cdot g \cdot R}\]
Oder anders herum, welcher Haftreibungskoeffizient in einer Kurve vorhanden sein muss, um diese mit einer bestimmten Geschwindigkeit durchfahren zu können:
\[\mu=\frac{v^2}{R \cdot g}\]
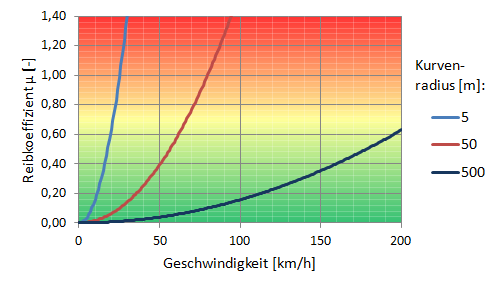
Weitere Informationen zu diesem Thema kann in [Stoffregen: Motorradtechnik] nachgeschlagen werden.
Die Berechnungen und Diagramme können in folgender Excel Tabelle nachvollzogen werden:
![]() Berechnungen zur Schräglage eines Motorrades
Berechnungen zur Schräglage eines Motorrades
Profis bei der Arbeit

Schaut man sich dieses Manöver im Vergleich zu den Berechnungen an, wird klar, was für ein Profi so ein Motorradfahrer ist. Nicht nur, dass er einen Ritt auf Messers Schneide der Physik unternimmt, im Video ist auch zu sehen, dass das Hinterrad einen erheblichen Antriebsschlupf aufweist, was noch zur Reduzierung der zur Verfügung stehenden Querkraft führt. In jedem Fall leisten die Reifen im Motorradrennsport einen wahnsinnigen Haftreibungskoeffizienten, wie er von Serienreifen nicht erreicht werden kann.
Bisheriger Rekord
Beispiele aus der gesamten Motorradwelt können in einem Artikel von Motorradonline angesehen werden.






7 Comments
Hallo,
zu Ihren Betrachtungen hinzuzufügen ist, dass der Fahrer in diesem Fall durch die Positionierung des Körpers den Schwerpunkt der Motorrad-Fahrer-Kombination von der in ihrem Bild gezeichneten gelben Linie weg bewegt.
Gruß
Konrad Heinze
Ja, absolut korrekt, das ändert aber nichts an der Kurvengeschwindigkeit oder dem Reibwert, sondern lediglich an der Neigung des Motorrades. Je mehr sich der Fahrer in die Kurve (und damit vom Motorrad weg) bewegt, desto geringer muss sich das Motorrad neigen, welches ja irgendwann mit Fußraste oder anderen Bauteilen aufsetzen würde.
Weiterführende Literatur z.B.: http://www.ifz.de/tipps%20und%20Tricks/ifz_Rastendruck.pdf
oder den angegebenen Stoffregen.
Bei diesem Modell besonders gut vorzustellen:
http://images.1000ps.net//images/berichte/f_G2355238.jpg?height=306&width460=&mode=crop
es ist bewiesen !
ENERGIE 1 = 1 , 6
das teil zieht ohne kraft !
TEST SELBER ! FAHRRAD
VF Felix Würth
bewiesen ; ZB AUTO , MOTORRAD !
mehr energie , wacht auf !
GOOGEL BILDER .
FELIX WÜRTH 2019
Sun Cellular
Smart Communications