Nachdem wir im Teil 1 den Kern des Kalman Filters geklärt haben, widmen wir uns nun dem komplizierteren Teil. Die im Teil 1 genannte Vorgehensweise mit dem multiplizieren bzw. addieren der Mittelwerte und Varianzen funktioniert so nur im eindimensionalen Fall. \(\)
Das heißt, wenn der Zustand, den man messen möchte, mit nur einer Variablen vollständig beschrieben werden kann. Das Beispiel, welches eingangs genannt wurde, die Position eines Fahrzeugs im Tunnel zu bestimmen, kann aber nicht mehr mit einer Variablen vollständig beschrieben werden. Zwar interessiert nur die Position, aber diese ist genau genommen ja schon 2-Dimensional in der Ebene (\(x\) & \(y\)). Außerdem kann nur die Geschwindigkeit (\(\dot x\) & \(\dot y\)) gemessen werden, nicht die Position direkt. Dies führt zu einem 4D-Kalman-Filter, mit folgenden Zustandsvariablen:
$$x=\begin{bmatrix}
x \\
y \\
\dot x \\
\dot y
\end{bmatrix}=\begin{matrix}\text{Position X} \\ \text{Position Y} \\ \text{Geschwindigkeit in X} \\ \text{Geschwindigkeit in Y}
\end{matrix}$$
Herr Kalman hatte sich nun überlegt, wie man es schafft, trotz verrauschter Messung einzelner Sensoren, eine optimale Schätzung aller Zustände zu berechnen.
Multidimensionales Kalman-Filter
Ich möchte die Vorgehensweise wieder am Beispiel eines Fahrzeugs mit Navigationsgerät, welches in einen Tunnel einfährt, erläutern. Die letzte bekannte Position ist vor dem Verlieren des GPS Signals. Danach steht (bei fest eingebauten Navis) nur noch die Geschwindigkeitsinformation vom Fahrzeug (Raddrehzahlen & Gierrate) als normalverteilte verrauschte Messgröße zur Verfügung. Daraus lässt sich eine Geschwindigkeit in \(x\) und \(y\) berechnen.
Anfangsbedingungen / Initialisierung
Systemzustand \(x\)
Zu Beginn muss man mit einem Ausgangszustand initialisieren. Im 1 Dimensionalen Fall war das \(\mu_0\), jetzt im mehrdimensionalen ein Vektor.
$$x_0=\begin{bmatrix}
x_0 \\
y_0 \\
\dot x_0 \\
\dot y_0
\end{bmatrix}$$
Ist nichts bekannt, können hier einfach 0 eingetragen werden. Sind schon einige Randbedingungen bekannt, können diese dem Filter mitgeteilt werden. Über die Wahl der nachfolgenden Kovarianzmatrix \(P\) steuert man, wie schnell das Filter auf die korrekten (gemessenen) Werte konvergiert.
Kovarianzmatrix \(P\)
Es muss eine Unsicherheit für den Ausgangszustand \(x_0\) angegeben werden. Im 1D Fall war das \(\sigma_0\), jetzt eine Matrix, welche für alle Zustände einzeln eine Unsicherheit zu Beginn definiert. Hier als Beispiel mit \(\sigma_0=10\) für alle 4 Zustände.
$$P=\begin{bmatrix}
10 & 0 & 0 & 0 \\
0 & 10 & 0 & 0 \\
0 & 0 & 10 & 0 \\
0 & 0 & 0 & 10
\end{bmatrix}$$
Diese Matrix wird wohl am Häufigsten während der Filterdurchläufe geändert. Sie wird sowohl im Predict als auch Correct Schritt geändert. Ist man sich über die Zustände zu Beginn ganz sicher, kann man hier niedrige Werte einsetzen, weiß man zu Beginn nicht genau, wie die Werte des Zustandsvektors sind, sollte die Kovarianzmatrix \(P\) mit sehr großen Werten (1 Million o.ä.) initialisiert werden, um dem Filter die Möglichkeit zu geben, relativ schnell zu konvergieren (die richtigen Werte auf Grund der Messungen zu finden).
Dynamikmatrix \(A\)
Der Kern des Filters ist allerdings nachfolgende Definition, welche man selbst nur mit großen Verständnis des physikalischen Zusammenhangs selbst aufstellen sollte. Für viele reale Probleme ist das nicht ganz einfach. Für unser einfaches Beispiel (Bewegung in der Ebene) ergibt sich die Physik dahinter aus der gleichmäßigen Bewegung. Für die Position ergibt sich \(x_{t+1}=\dot x_t \cdot t + x_t\) und für die Geschwindigkeit \(\dot x_{t+1}=\dot x_t\). Für den oben dargestellten Zustandsvektor ist die Dynamik in Matrizenschreibweise nachfolgende:
$$A=\begin{bmatrix}
1 & 0 & dt & 0 \\
0 & 1 & 0 & dt \\
0 & 0 & 1 & 0 \\
0 & 0 & 0 & 1
\end{bmatrix}$$
Diese sagt aus, “wohin” sich der Zustandsvektor von einem Berechnungsschritt zum nächsten innerhalb \(dt\) bewegt. Dieses Dynamikmodell wird auch “Constant Velocity” Modell genannt, weil es davon ausgeht, dass während eines Berechnungsschritts des Filters die Geschwindigkeit konstant bleibt.
$$\begin{bmatrix}
x \\
y \\
\dot x \\
\dot y
\end{bmatrix}_{t+1}=\begin{bmatrix}
1 & 0 & dt & 0 \\
0 & 1 & 0 & dt \\
0 & 0 & 1 & 0 \\
0 & 0 & 0 & 1
\end{bmatrix}\cdot \begin{bmatrix}
x \\
y \\
\dot x \\
\dot y
\end{bmatrix}_t$$
Als Beispiel nur mal die 1. Zeile ausgeschrieben, welche die Position nach einem Berechnungsschritt mit der Zeitdauer \(dt\) berechnet.
$$x_{t+1}=x_t+dt\cdot \dot x_t$$
Dies spiegelt einfach physikalische Zusammenhänge für die gleichförmige Bewegung wider. Eine höhere Form wäre das Constant Acceleration Modell, welches ein 6D Filter wäre und noch die Beschleunigungen imZustandsvektor beinhaltet. Hier kann man prinzipiell auch andere Dynamiken vorgeben (z.B. ein holonomes Fahrzeug).
Prozessrauschkovarianzmatrix \(Q\)
Da die Bewegung des Fahrzeugs ebenfalls gestört (im Sinne von überlagertem, normalverteiltem Rauschen) sein kann, wird dies über die Prozess-Rausch-Kovarianzmatrix \(Q\) eingebracht. Diese Matrix teilt dem Filter mit, wie der Systemzustand von einem zum nächsten Schritt “springen” kann. Stellen wir uns das Fahrzeug vor, welches fährt. Dieses kann von einem Windstoß oder Straßenunebenheiten gestört werden, was eine Krafteinwirkung zur Folge hat. Eine Geschwindigkeitsänderung durch den Fahrer ist ebenfalls eine Beschleunigung, welche auf das Fahrzeug wirkt. Wirkt nun eine Beschleunigung auf den Systemzustand \(x\) ein, so ist die physikalische Abhängigkeit dafür
$$x = \frac{1}{2}dt^2 \cdot \ddot x$$
$$\dot x = dt \cdot \ddot x$$
Die Matrix \(Q\) ist eine Kovarianzmatrix, welche folgende Elemente enthält:
$$Q = \begin{bmatrix}\sigma_{x}^2 & \sigma_{xy} & \sigma_{x \dot x} & \sigma_{x \dot y} \\ \sigma_{yx} & \sigma_{y}^2 & \sigma_{y \dot x} & \sigma_{y \dot y} \\ \sigma_{\dot x x} & \sigma_{\dot x y} & \sigma_{\dot x}^2 & \sigma_{\dot x \dot y} \\ \sigma_{\dot y x} & \sigma_{\dot y y} & \sigma_{\dot y \dot x} & \sigma_{\dot y}^2 \end{bmatrix}$$
Sie lässt sich am einfachsten berechnen, in dem man den Vektor \(G\) aufstellt und diesen nachfolgend mit der angenommenen Standardabweichung für die angreifende Beschleunigung multipliziert, z.B. \(\sigma_a=8m/s^2\).
$$Q = G\cdot G^T \cdot \sigma_a^2$$
mit \(G = \begin{bmatrix}0.5 \Delta t^2 & 0.5 \Delta t^2 & \Delta t & \Delta t\end{bmatrix}^T\).
Steuermatrix \(B\) und Steuergröße \(u\)
Auch ein Einwirken externer Steuergrößen (z.B. Lenken, Bremsen, etc.) ist über die Steuermatrix \(B\) möglich, soll hier aber zur einfacheren Erläuterung weg gelassen werden.
Messmatrix \(H\)
Dem Filter muss ebenfalls mitgeteilt werden, was gemessen wird und in welchem Verhältnis es zum Zustandsvektor steht. Im Beispiel des Fahrzeugs, was in einen Tunnel einfährt, nur die Geschwindigkeit, nicht mehr die Position! Die Werte sind direkt mit dem Faktor 1 messbar (d.h. es wird direkt die Geschwindigkeit in der richtigen Einheit gemessen), weshalb in \(H\) nur 1.0 an entsprechende Stelle gesetzt wird.
$$H=\begin{bmatrix}
0 & 0 & 1 & 0\\
0 & 0 & 0 & 1
\end{bmatrix}$$
Messen die Sensoren in einer anderen Einheit oder die Größe über Umwege, müssen die Zusammenhänge in der Messmatrix \(H\) formelmäßig abgebildet werden.
Messrauschkovarianzmatrix \(R\)
Wie auch schon im eindimensionalen Fall die Varianz \(\sigma_0\), muss hier ebenfalls eine Messunsicherheit angegeben werden.
$$R=\begin{bmatrix}
10 & 0\\
0 & 10
\end{bmatrix}$$
Diese Messunsicherheit gibt an, wie sehr man den Messwerten der Sensoren vertraut. Da wir nur \(\dot x\) und \(\dot y\) messen, ist dies eine 2×2 Matrix. Ist der Sensor sehr genau, so sollten hier kleine Werte eingesetzt werden. Ist der Sensor relativ ungenau, so sollten hier große Werte eingesetzt werden.
Einheitsmatrix \(I\)
Zu guter letzt ist noch eine Einheitsmatrix notwendig.
$$I=
\begin{bmatrix}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 0 & 0 & 1
\end{bmatrix}$$
Filterschritt Vorhersagen/Predict
Dieser Teil des Kalman-Filter wagt nun eine Vorhersage des Systemzustands in die Zukunft. Außerdem kann mit ihm unter bestimmten Voraussetzungen (Beobachtbarkeit) auch ein Zustand berechnet werden, welcher nicht gemessen werden kann! Das ist erstaunlich, aber für unseren Fall genau das, was wir benötigen. Die Position des Fahrzeugs können wir ja nicht messen, denn das GPS des Navigationsgeräts hat in einem Tunnel keinen Empfang. Durch die Initialisierung des Zustandsvektors mit einer Position und der Messung der Geschwindigkeit, kann aber mit der Dynamik \(A\) dennoch eine optimale Vorhersage über die Position getroffen werden.
$$x_{t+1}=A \cdot x_t$$
Die Kovarianz \(P\) muss ebenfalls neu berechnet werden. Die Unsicherheit über den Zustand des Systems wird im Predict Schritt größer, wie man im 1D Fall einfach gesehen hat. Im mehrdimensionalen Fall kommt die Messunsicherheit \(Q\) additiv hinzu, die Unsicherheit \(P\) wird also immer größer.
$$P=A \cdot P \cdot A’ + Q$$
Das war’s schon. Wir haben in die Zukunft (\(dt\)) gerechnet. Das Kalman-Filter hat eine Aussage über den erwarteten Systemzustand in der Zukunft getroffen.
Jetzt vergeht genau \(dt\) Zeit und das Filter ist im Messen/Korrigieren und überprüft, ob die Vorhersage des Systemzustands gut zu den neuen Messwerten passt. Wenn ja, wird die Kovarianz \(P\) vom Filter geringer gewählt (es ist sich sicherer), wenn nicht, größer (irgendwas stimmt nicht, das Filter wird unsicherer).
Filterschritt Messen/Korrigieren
Die nun folgenden mathematischen Berechnungen sind nichts, was man zwingend herleiten können muss. Das hat sich der Rudolf E. Kalman in ein paar ruhigen Minuten überlegt und es sieht verrückt aus, aber funktioniert.
Von den Sensoren kommen aktuelle Messwerte \(Z\), mit welchen eine Innovation \(w\) des Zustandsvektors \(x\) mit der Messmatrix \(H\) berechnet wird.
$$w=Z-(H \cdot x)$$
Anschließend wird geschaut, mit welcher Varianz (welche im mehrdimensionalen Fall Kovarianzmatrix heißt) weiter gerechnet werden kann. Dafür wird die Unsicherheit \(P\) sowie die Messmatrix \(H\) und die Messunsicherheit \(R\) benötigt.
$$S=(H \cdot P \cdot H’+R)$$
Damit wird das so genannte Kalman-Gain bestimmt. Es sagt aus, ob den Messwerten oder der Systemdynamik mehr vertraut werden soll.
$$K=\frac{P \cdot H’}{S}$$
Das Kalman Gain wird geringer, wenn die Messwerte dem vorhergesagten Systemzustand entsprechen. Sollten die Messwerte völlig anderes aussagen, so werden die Elemente der Matrix K größer.
Mit diesen Informationen wird jetzt der Systemzustand geupdated.
$$x=x+(K\cdot w)$$
Und auch eine neue Kovarianz für den kommenden Predict Schritt bestimmt.
$$P=(I-(K \cdot H)) \cdot P$$
Nun geht es wieder in den Schritt Prediction. Grafisch sieht das so aus:
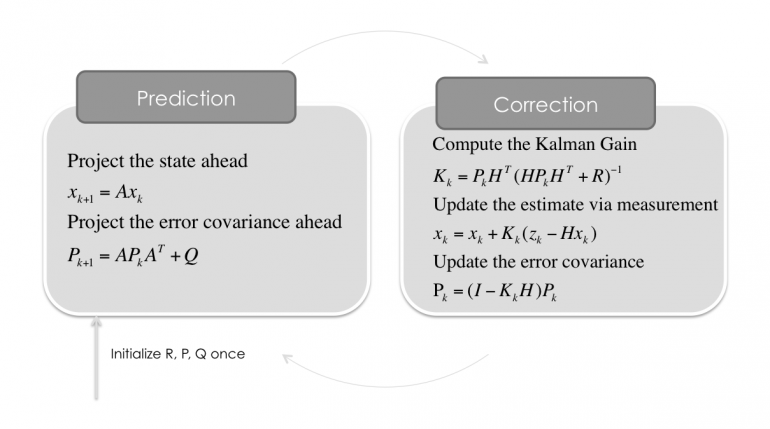
Dieses Filter läuft dauerhaft, so lange Messwerte herein kommen. Es kann auch ‘Open Loop’ betrieben werden, also nur der Prediction Schritt wird ausgeführt, wenn keine Messwerte zur Verfügung stehen. Dann wird die Unsicherheit \(P\) allerdings immer größer.
Matlab Implementierung eines mehrdimensionalen Kalman Filters
% Paul Balzer | Motorblog
% CC-BY-SA2.0 Lizenz
clear all; clc
%% Messungen generieren
% Da wir jetzt keine Messwerte haben,
% generieren wir uns einfach selbst
% ein paar verrauschte Werte.
it=100; % Anzahl Messwerte
realv=10; % wahre Geschwindigkeit
% x' y'
measurements = [realv+1.*randn(1,it); zeros(1,it)];
dt = 1; % Zeitschritt
%% Initialisieren
% x y x' y'
x = [0; 0; 10; 0]; % Initial State (Location and velocity)
P = [10, 0, 0, 0;...
0, 10, 0, 0;...
0, 0, 10, 0;...
0, 0, 0, 10]; % Initial Uncertainty
A = [1, 0, dt, 0;...
0, 1, 0, dt;...
0, 0, 1, 0;...
0, 0, 0, 1]; % Transition Matrix
H = [0, 0, 1, 0;...
0, 0, 0, 1]; % Measurement function
R = [10, 0;...
0, 10]; % measurement noise covariance
Q = [1/4*dt^4, 1/4*dt^4, 1/2*dt^3, 1/2*dt^3;...
1/4*dt^4, 1/4*dt^4, 1/2*dt^3, 1/2*dt^3;...
1/2*dt^3, 1/2*dt^3, dt^2, dt^2;...
1/2*dt^3, 1/2*dt^3, dt^2, dt^2]; % Process Noise Covariance
I = eye(4); % Identity matrix
%% Kalman Filter Steps
%
for n=1:length(measurements)
% Prediction
x=A*x; % Prädizierter Zustand aus Bisherigem und System
P=A*P*A'+Q; % Prädizieren der Kovarianz
% Correction
Z=measurements(:,n);
y=Z-(H*x); % Innovation aus Messwertdifferenz
S=(H*P*H'+R); % Innovationskovarianz
K=P*H'*inv(S); % Filter-Matrix (Kalman-Gain)
x=x+(K*y); % aktualisieren des Systemzustands
P=(I-(K*H))*P; % aktualisieren der Kovarianz
end
Das Filter bei der Arbeit
Nehmen wir nun also an, dass wir mit \(\dot x=10m/s\) in einen Tunnel fahren und die letzte bekannte Position \(x=0, y=0\) ist. Dann ermittelt das Kalman Filter die Position des Fahrzeugs, obwohl diese gar nicht gemessen werden kann. In der nachfolgenden Abbildung mal für 6 Filterdurchläufe:

Man sieht, wie sich das Filter über die aktuelle Position immer unsicherer wird (Kurve links oben wird flacher), über die gefahrene Geschwindigkeit allerdings immer sicherer (Kurve rechts oben wird immer schmaler). Die Geschwindigkeitsmessung ist aber auch immer sehr exakt 10m/s, wodurch die Innovation sehr klein wird, das Filter also nicht viel korrigieren muss.
Da die Fahrzeuggeschwindigkeit über den CAN-Bus ca. alle 20ms zur Verfügung steht, entsprechen 6 Iterationen nur reichlich 0.1s. Das Filter konvergiert, je nach Wahl der Anfangsbedingungen, relativ schnell. Beispielsweise ist nach 100 Iterationen (entspricht 2s auf dem Fahrzeug) die Varianz schon sehr gering, das Filter ist sich also ziemlich sicher, dass es richtig liegt.
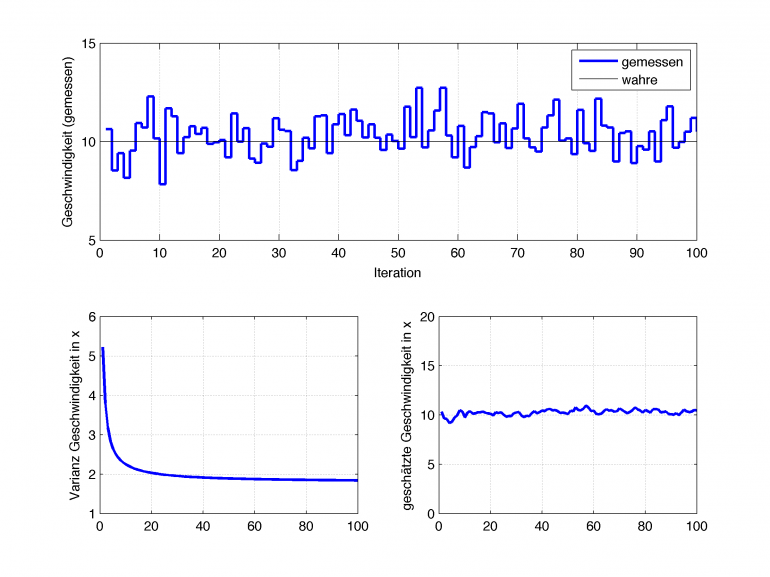
oben: gemessene Geschwindigkeit, links: Varianz der Geschwindigkeit, rechts: geschätzte Geschwindigkeit
Python Implementierung des Kalman Filters
Falls Matlab nicht zur Verfügung steht, hier eine Beispielimplementierung in Python.
import numpy as np
for n in range(len(measurements[0])):
# Time Update (Prediction)
# ========================
# Project the state ahead
x = A*x
# Project the error covariance ahead
P = A*P*A.T + Q
# Measurement Update (Correction)
# ===============================
# Compute the Kalman Gain
S = H*P*H.T + R
K = (P*H.T) * np.linalg.pinv(S)
# Update the estimate via z
Z = measurements[:,n].reshape(2,1)
y = Z - (H*x) # Innovation or Residual
x = x + (K*y)
# Update the error covariance
P = (I - (K*H))*P
Der Python Code aus dem Video ist auf balzer82.github.io/Kalman zu finden.
Filterdesign: Wie wähle ich Q und R?
Insgesamt ist egal wie groß die Zahlenwerte in \(Q\) und \(R\) sind, vielmehr ist entscheidend in welchem Verhältnis sie stehen. Wird \(R\) zehnfach größer gewählt und \(Q\) ebenfalls, so wird das im Filter kaum Auswirkungen haben. Das Verhältnis der Werte ist entscheidend. Die korrekte Wahl von \(Q\) und \(R\) sind direkt für die Filterperformance verantworlich und bilden die grundlegende Frage des Filterdesigns:

Diese Entweder/Oder Fragestellung kann nur anwendungsspezifisch entschieden werden. In einigen Fällen möchte man einfach schlecht messende Sensoren für einen relativ konstanten Prozess filtern, im anderen Fall will man mehrere Sensoren fusionieren und die Dynamik soll erhalten bleiben. Demnach sind die Matrizen zu wählen. Alternativ kann natürlich auch das Filter Adaptiv ausgelegt werden, d.h. \(Q\) oder/und \(R\) können im laufenden Betrieb geändert werden.
Fazit
Das Kalman-Filter ist relativ schnell und einfach zu implementieren und liefert für normalverteilte verrauschte Sensorwerte unter gewissen Voraussetzungen (nicht näher erläutert) eine optimale Schätzung des Zustands. Herr Kalman war von seinem Algorithmus so überzeugt, dass er auch einen befreundeten Ingenieur bei der NASA begeistern konnte. Und so half dieses Filter erstmals im Apollo Guidance Computer bei den Mondlandungen.
Ach übrigens: Für kommerzielle Anfragen gibt es auch die Möglichkeit mich zum Thema zu konsultieren. Hire me!
Errata
02/2014: In vorheriger Version war ein Fehler: Im Matlab Code waren die Update/Predict Schritte vertauscht.
03/2014: Die Erläuterung wurde noch mal überarbeitet. Python Implementierung eingefügt
07/2016: Travolta Filter Design Tradeoff hinzugefügt





36 Comments
Danke für den großartigen Artikel, welcher mir bei der Implementierung eines Kalman Filters weitergeholfen hat.
Während meiner Recherchen ist mir aufgefallen, dass in dem hier vorgestellten Kalman-Filter offenbar ein paar Vereinfachungen vorgenommen wurden.
Wikipedia gibt noch eine Dynamik B für die externen Einflüsse u an.
Viel wichtiger (zumindest für meine Anwendung) ist jedoch, dass die Unsicherheit (bei Wikipedia und anderen Quellen mit Q angegeben) der Systemdynamik F hier fehlt.
Beim einfachen Filtern von Sensordaten mit dem hier vorgestellten Filter muss ich manuell die Unsicherheit P des Zustandes regelmäßig zurücksetzen um einen, den tatsächlichen Daten folgenden, Verlauf des Filters zu erreichen. Durch das Hinzufügen von Q entfällt dieser hack.
Die notwendige Änderung ist im Vorhersagen/Predict Schritt:
x = F * x + B*u
P = F * P *F^T + Q
Hallo Martin,
du hast Recht. Ich habe es zu einfach gemacht, weshalb das nicht so ganz korrekt war. Ich habe die Matrix Q noch eingefügt und auch erläutert, wie diese zustande kommt.
Jetzt ist es etwas komplizierter aber dafür fast vollständig (bis auf B und u).
Hallo,
kurze Frage zum Verständnis: Die Varianz passt sich der Ungenauigkeit an. Sprich: Wenn der Unterschied zwischen Messung und Schätzung sehr groß ausfällt, müsste ja die Streuung/Varianz der nächsten Schätzung größer ausfallen. Wo ist aber der Zusammenhang zwischen der Varianz und dem Fehler bzw. der Schätzung? Rein mathematisch betrachtet, errechnet er mir die neue Varianz über die letzte Varianz + Unsicherheit der Messung (ungefähre Vorstellung zumindenst) Ich sehe jedoch darin keine Abhängigkeit von der Messung z oder der neuen Schätzung…
“Das Kalman Gain wird geringer, wenn die Messwerte dem vorhergesagten Systemzustand entsprechen. Sollten die Messwerte völlig anderes aussagen, so werden die Elemente der Matrix K größer.”
Nur noch als Zitat wo mein Problem ist….? Wo ist der der mathematische Zusammenhang zwischen dem Kalman Gain und den Messwerten? Der Kalman Gain wird ja über die vorherigen geschätzten Varianzen errechnet…diese haben aber keine Aussagekraft über die Messungen. (mathem. unabh, oder?)
Ich habe auch Verständnisprobleme mit dieser Formulierung (Kalman Gain).
In meiner Simulation konvergiert der Kalmangain nach x Iterationen immer auf einen festen Wert.
Dann muss ich ja diesen stationären Wert nur einmalig bestimmen und spare mir so viel Rechenleistung bei der Implementierung in Echtzeitsystemen (compute the kalman gain und update the error covariance fallen dann weg??)
Da muss es doch irgendwo einen Haken geben???
Hallo Lukas,
also nehmen wir an ein Messwert haut völlig daneben. Dann ist die geschätzte Varianz P für diesen Systemzustand hoch. Damit wird das Kalman Gain klein, somit der Messwert nicht mehr so stark gewichtet wie die Systemdynamik.
Das P (also die Measurement Covariance Matrix) wird ja vom Update/Predict Schritt hin&her gereicht.
Schau mal hier, da ist es noch mal etwas anders erklärt: http://youtu.be/NT7nYv9Ri2Y?t=10m49s
Hallo Paul, Lukas und Kai,
ich Versuche selbst seit paar Tagen aus dem Kalman Filter schlau zu werden und bin ebenfalls genau an dieser Frage hängen geblieben was denn nun wirklich Einfluß auf K hat. Wenn man sich die Formeln genau ansieht kann man aber auch ohne alles im Detail zu verstehen feststellen dass die Formeln aus denen K und P berechnet wird ein “geschlossenes” System darstellen in dem die Innovation (also die Differenz zwischen Schätzwert und Messwert) gar nicht vorkommt und somit auch keinen Einfluss haben kann.
Der Satz:
“Das Kalman Gain wird geringer, wenn die Messwerte dem vorhergesagten Systemzustand entsprechen…..”
stimmt also so wie er da steht nicht bzw. ist sehr missverständlich. Tatsächlich ist es wohl so wie auch Kai sagt: Wenn Q und R Konstanten sind, verändern sich K und P nach einigen Iterationen nicht mehr und können (wenn der Startzustand von P nicht variabel zu sein braucht) offline vorherberechnet werden.
Siehe dazu auch Wikipedia ( http://de.wikipedia.org/wiki/Kalman-Filter) am Ende des Abschnitts “Korrektur”
Anders sieht es aus wenn sich R (die Varianz der Messwerte) über die Zeit ändert und diese Änderung online berücksichtig werden soll – diese Änderung müsste man aber erstmal mitkriegen bzw. zusätzlich modellieren.
Korrekt.
Mal ne blöde Frage.
Im Bild steht unter
“Update the estimate via measurement”
Xk = Xk + Kk(…)
Dabei kürzt sich Xk doch raus. Müsste links nicht Xk+1 stehen?
Gruß Peter
Hallo Peter,
keine blöde Frage! Völlig richtig. Ich habe das weg gelassen, um die Formeln so einfach wie möglich zu machen und sie ähnlich dem zu implementierenden Code zu gestalten.
Rein mathematisch hast du natürlich Recht! Im Code allerdings ist es die gleiche Variable, die einfach überschrieben wird. Mir hatte das damals viel geholfen, das so zu sehen.
Es ist immer ein schmaler Grad, Dinge aus didaktischen Gründen weg zu lassen und so korrekt zu bleiben, dass es nicht falsch ist.
Wenn du dir Bücher von Universitätsprofessoren anschaust, dann wirst du fest stellen, dass da zwar immer alles mathematisch völlig korrekt ist, man aber die 10fache Zeit braucht, um das zu verstehen. :)
Ging mir zumindest so.
Hallo,
erstmal vielen Dank für die übersichtlich gestaltete Seite zum Kalman-Filter.
Ich möchte den Kalman-Filter einsetzen, um ein Rauschen zu elimieren:
Und zwar habe ich die x-und y-Positionen von Fahrzeugen und Fußgängern mit einem Laserscanner aufgezeichnet. Aus den gemessenen Positionen und der Zeit kann ich die Geschwindigkeiten ermitteln.
Jetzt will ich die vom Laserscanner aufgezeichneten Positionen im Koordinatensystem filtern, um einen realen Fahreugbewegungsverlauf zu erhalten, da sich durch die Aufzeichnung mit dem Laserscanner eine unwahrscheinliche Bewegung ergibt.
Meine Frage dazu:
Was muss ich verändern, um die Position und nicht die Geschwindigkeit als gegeben anzusehen?
Und was muss ich für die “measurements” angeben? Die Definition habe ich nämlich noch nicht ganz verstanden.
Vielen Dank im Voraus
Danke für die ausführliche Erklärungen. Dennoch habe ich ein Paar Anmerkungen zu den Schreibweisen:
Sie haben das zweite Differential als dt^2 angegeben. Sollte es nicht d^2t heißen?
Sie verwechseln zum Teil das Gleichheitszeichen der Mathematik mit dem der üblichen Programmiersprachen.
Gleichheitszeichen in der Programmierung wird für eine Zuweisung, assignment verwendet. D.h. x=3 heißt, dass x den Wert 3 annehmen soll.
Ein Gleichheitszeichen in der Mathematik (=) ist eine “Wahrheit”, ein Statement. Der Ausdruck x=3 bedeutet, dass x gleich 3 ist. Das bedeutet, eine Schreibweise “x=x+3” ist mathematisch fehlerhaft, wohingegen sie programmiererisch Sinn macht.
Sie haben solche Ausdrücke wie “x=A *x”, welche nicht sinnvoll sind. Dafür gäbe es z.B. Zuweisungszeichen wie “:=” (x:=A*x), was wiederrum sehr ungünstig bei solchen Beschreibungen sind, wenn Sie die Bedeutung der Zeichen im Laufe der Scripting ändern. Am schönsten fände ich es, wenn Sie mit Sub- und Superskripten arbeiten würden. Somit sind die mathematischen Beschreibungen auch richtig”er”.
Nichts für Ungut. Sehr nette Erklärungsweise bis auf ein Paar “Kleinigkeiten”.
Vielen Dank für die sehr anschauliche Beschreibung.
Für mich stellt sich nun folgende Frage:
Angenommen ich habe zwei Sensoren. Einer davon kann in regelmäßigen Abständen gelesen werden (zB Geschwindigkeitssensor), während der andere unregelmäßig misst (zB GPS-Sensor).
Kann ich nun beide Sensoren miteinander vereinen, indem ich je nach empfangenen Sensor die Messrauschkovarianzmatrix R und die Messmatrix H vor jedem Correction-Schritt entsprechend anpasse?
Oder müssen diese Matrizen immer konstant bleiben?
Vielen Dank im Voraus!
Hi Leo,
super verstanden und genau richtig gedacht! Du stellst in dem Fall einfach in der Measurement Matrix H an der betreffenden Stelle eine 1 oder 0 ein.
Wenn GPS Messung da ist, eine 1 und wenn kein GPS da ist eine 0. Der Rest bleibt alles so.
Habe ich z.B. beim Extended Kalman Filter so gemacht.
Hi,
wenn meine gemessenen Größen Position(X,Y), Beschleunigung(X,Y) und die Drehrate sind,
kann ich dann einfach den Zustandsvektor x zu [X, Y, X_p, Y_p, X_pp, Y_pp, Drehrate] erweitern?
Benötige ich dann in diesem Fall den Erweiterten KF mit dem Eingangsvektor u um meine Drehrate abhängig vom Lenkwinkel/Rotationswinkel zu bestimmen?
Vielen Dank im Voraus :)
Hallo,
inwieweit würde sich denn das Filter respektive die Gleichungen ändern, wenn man keine gleichförmige Bewegung hätte, sondern bewusst beschleunigt oder bremst?
Hallo Robert,
im einfachsten Fall würdest du den ‘State Vector’ noch um diese Dynamikanteile erweitern, also z.B.
$$x=\begin{bmatrix}
x \\
y \\
\dot x \\
\dot y \\
\ddot x \\
\ddot y
\end{bmatrix}$$
als Zustandsvektor nutzen. Oder du bringst (hier nicht gezeigt) die Beschleunigung als ‘Driver’ mit rein, lässt also den neuen Zustandsvektor \(\dot x\) mit \(Ax + Bu\) prädizieren, dann wäre die Beschleunigung in \(u\).
Hey Leute,
Ich wollte mir die Wahrscheinlichkeiten für die Geschwindigkeit plotten und stoße dabei auf kleine Hindernisse.
Code:
xAxis=[-5:0,1:25];
plot(xAxis, normpdf(xAxis,x(3),P(3,3)))
Eingefügt habe ich den plot-Befehl vor dem “end” der Schleife. Das x(3) ist mein geschätzter Mittelwert für den Zeitschritt, um den ich mit meiner Varianz P(3,3) die Normalverteilung bilden möchte. Es funktioniert auch soweit, dass ich einen plot um meine Geschwindigkeit von ca. 10m/s bekomme. Nur leider stimmen die Wahrscheinlichkeiten nicht mit denen des plott’s oben überein. Siehst jemand meinen Fehler?
Danke euch :)
Der Plot wurde mit dt=0.1s gemacht !!
Hallo Paul,
ich bin gerade dabei dein Programm mal in Matlab nachzuvollziehen. Ich bin was Matlab angeht noch nicht so fit darin.
Was muss ich denn noch machen, damit ich den Filter bei der Arbeit sehen kann.
der Befehl “Plot” wäre doch eine Möglichkeit oder?
Vielleicht kannst du oder jemand anderes mir weiterhelfen.
Liebe Grüße
Lars
Hallo Paul,
Wie hast du die Gausskurven für Geschwindigkeit und
Position in Matlab geplottet ?
Für die Geschwindigkeit:
…..
…..
x=x+(K*y); % aktualisieren des Systemzustands
P=(I-(K*H))*P; % aktualisieren der Kovarianz
if(n<=6)
mu=x(3); sigma=P(3,3);
pd=makedist('normal','mu',mu,'sigma',sigma)
x1=-10:0.1:30; y=pdf(pd,x1);
plot(x1,y)
hold on
end
Für die Position:
…..
…..
x=x+(K*y); % aktualisieren des Systemzustands
P=(I-(K*H))*P; % aktualisieren der Kovarianz
if(n<=6)
mu=x(1); sigma=P(1,1);
pd=makedist('normal','mu',mu,'sigma',sigma)
x1=-10:0.1:120; y=pdf(pd,x1);
plot(x1,y)
hold on
end
Für die Position:
…..
…..
x=x+(K*y); % aktualisieren des Systemzustands
P=(I-(K*H))*P; % aktualisieren der Kovarianz
if(n<=6)
mu=x(3); sigma=P(3,3);
pd=makedist('normal','mu',mu,'sigma',sigma)
x1=-10:0.1:30; y=pdf(pd,x1);
plot(x1,y)
hold on
end
Hallo Paul,
Dein Artikel ist für mich recht schwierig nachzuvollziehen, weil ständig irgendwelche Gleichungen ohne weiteren Kommentar vom Himmel fallen und ich dann versuche, Begründungen dafür zu finden (ah, ja, bedingte Wahrscheinlichkeiten, der Satz von Bayes, daher die entsprechende Gewichtung … )
Manche Gleichungen sind sehr erstaunlich.
Du hast da eine Prozeßrauschkovarianzmatrix (4 x 4) und einen Vektor G und schreibst:
Q=G⋅GT⋅σ2a, wobei σ2a eine reelle Zahl ist.
Was soll das sein?
Welche Verknüpfung ist zwischen G und GT?
Da kommt doch nie im Leben ne Matrix bei raus …
Wenn Du irgendwas nicht erklären willst, dann lass es weg, das spart dann Deinen Lesern die Nerven.
So bin ich zumindest stundenlang am recherchieren, um Deinen Artikel auf mathematisch korrekte Beine zu stellen,
Viele Grüße,
Jutta
Hi Jutta, natürlich setzt der Artikel ein gewisses Vorwissen voraus, welches ohnehin notwendig ist um ein Kalman Filter in dem gewünschten, eigenen Kontext umsetzen zu können. Daher ist deine Logik noch weniger Informationen im Artikel zu haben, eher kontraproduktiv, weil man sonst noch länger damit beschäftigt wäre, die relevanten mathematischen Zusammenhänge zusammenzu suchen.
Artikel mit gröberen Erklärungen zum Kalman Filter gibt es ja auch genug im Internet.
Der Vektor G beschreibt den Zusammenhang zwischen zwischen der potentiell möglich angreifenden Beschleunigung (welche als Störung (Varianz) der Zustandsgrößen zu verstehen ist) und der Zustandsgrößen wieder.
Die Varianz in m/s^2 kann integriert werden, sodass die Einheiten der einzelnen Zustandsgrößen wieder passen. Deswegen sind die ersten zwei Elemente von G 0.5*t^2 und die letzten zwei nur t.
Der Vektor G (4×1) und seine Transponierte G_t (1×4) können jetzt multipliziert werden, um die Zusammenhänge zwischen dieser Störung (σ_a)^2 und den Kovarianzen zwischen allen Zustandsgrößen herzustellen. [Wie die Varianzen angegeben werden (oder deren Einheit) sollten bekannt sein, da ein Kalman Filter im Prinzip genau darauf basiert]
Der Wert für (σ_a)^2 ist hier willkürlich gewählt, konstant, um es einfacher zu machen.
Durch die Vektordimension von G kommt dabei eine Matrix 4<4 raus.
оптовая продажа цветов в Волгограде – https://lepestok.su/optovaya-prodaja-semyan-online