Dynamik eines Viertelfahrzeugs

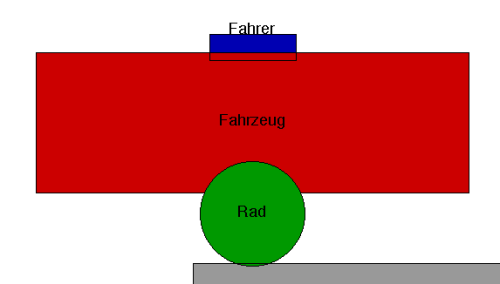
Ein sehr simples Abstraktionsmodell um die Dynamik eines Fahrzeugs in vertikaler Richtung zu simulieren ist die Reduktion auf ein 1/4-Fahrzeug-Modell. Das heißt, dass das Fahrzeug in Längsrichtung geteilt wird (2 Räder + Nickbewegung) und dann nochmal in Querrichtung. Somit bleibt ein Rad mit entsprechender Federung und Stoßdämpfern, 1/4 der Fahrzeugmasse und 1/4 des Fahrers übrig.

Interessant ist nun die Fragestellung, welche Eigenfrequenzen das System hat und wie es auf Bodenwellen reagiert. Außerdem kann man die Auswirkung von defekten Stoßdämpfern auf die Schwingung berechnen.

Bewegungsgleichungen für ein Drei-Massen-Feder-Dämpfer-Modell

Diese sind wunderbar in [Mitschke – Dynamik der Kraftfahrzeuge] beschrieben. Diese Nomenklatur möchte ich gleich übernehmen.

Die Differentialgleichungen sollen nun numerisch “gelöst” werden. Dazu müssen diese in eine Form gebracht werden, welche einfach mit geeigneter Software berechnet werden kann. Prinzipiell ginge dies sogar mit Excel, allerdings wird es bei komplexeren Systemen zunehmend komplizierter. Daher soll auf den unangefochtenen Marktführer für mathematische Berechnungen, Mathworks Matlab zurück gegriffen werden.

3-Massen-Feder-Dämpfer Viertelfahrzeug im Zustandsraummodell

Die einfachste Möglichkeit ein System zu beschreiben ist in Form eines Zustandsraummodells. Dazu werden die Differentialgleichungen auf Differentialgleichungen 1. Ordnung reduziert. Mit der Nomenklatur von [Mitschke] ist der Zustand des 3-Massen-Feder-Dämpfer Viertelfahrzeugs mit folgendem Zustandsvektor \(\vec x\) vollständig beschrieben.

\[\vec x=\begin{bmatrix}z_1 \\ \dot z_1 \\ z_2 \\ \dot z_2 \\ z_3 \\ \dot z_3 \end{bmatrix}=\begin{bmatrix}\text{Vertikalbewegung des Rades} \\ \text{Vertikalgeschwindigkeit des Rades} \\ \text{Vertikalbewegung des Aufbaus} \\ \text{Vertikalgeschwindigkeit des Aufbaus} \\ \text{Vertikalbewegung des Fahrers} \\ \text{Vertikalgeschwindigkeit des Fahrers} \end{bmatrix}\]

Sind die Position und die Geschwindigkeit von Rad, Aufbau und Fahrer bekannt (6 Variablen), so ist das dynamische System vollständig beschrieben. Der Vektor x stellt den Zustand dar.

Ein Zustandsraummodell ist allgemein in der Form

\[\dot x=\boldsymbol{A} \cdot x + \boldsymbol{b} \cdot h\]

Dabei ist A die Systemmatrix in welcher die Dynamik beschrieben wird. Als b wird der Steuervektor bezeichnet, welcher beschreibt wie die Änderung von h (in diesem Fall die Unebenheit der Straße) auf das System wirkt.

Die Vorgehensweise zur Erstellung eines Zustandsraummodells aus Differentialgleichungen basiert auf Matrizenrechnung.

\[\begin{bmatrix}\dot z_1 \\ \ddot z_1 \\ \dot z_2 \\ \ddot z_2 \\ \dot z_3 \\ \ddot z_3 \end{bmatrix} = \begin{bmatrix}0 & 1 & 0 & 0 & 0 & 0 \\ -\frac{(c_2+c_1)}{m_1} & -\frac{k_2}{m_1} & \frac{c_2}{m_1} & \frac{k_2}{m_1} & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 \\ \frac{c_2}{m_2} & \frac{k_2}{m_2} & -\frac{(c_3+c_2)}{m_2} & -\frac{(k_3+k_2)}{m_2} & -\frac{c_3}{m_2} & \frac{k_3}{m_2} \\ 0 & 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & \frac{c_3}{m_3} & \frac{k_3}{m_3} & -\frac{c_3}{m_3} & -\frac{k_3}{m_3} \end{bmatrix} \cdot \begin{bmatrix} z_1 \\ \dot z_1 \\ z_2 \\ \dot z_2 \\ z_3 \\ \dot z_3 \end{bmatrix} + \begin{bmatrix}0 \\ \frac{c_1}{m_1} \\ 0 \\ 0 \\ 0 \\ 0 \end{bmatrix} \cdot h\]

Die für die Simulation nötigen Matrizen \(C\) (Beobachtungsvektor) und \(D\) (Durchgriffsvektor) sind:

\[\vec c=\begin{bmatrix}0 & 0 & 0 & 0 & 0 & 0\end{bmatrix}\]
\[d=\begin{bmatrix}0\end{bmatrix}\]

Je nachdem welche Spalte im Beobachtungsvektor mit 1 belegt wird, kann Bewegung oder Geschwindigkeit von Rad, Aufbau oder Fahrer “beobachtet” werden. Das System ist nun vollständig beschrieben und kann mit Matlab berechnet werden.

Numerische Berechnung mit Matlab

% check ob Toolbox installiert ist für Zustandsraummodell
if exist('ss')==2
  disp('System Control Toolbox ist installiert')
else
  disp('System Control Toolbox wird benötigt')
  return
end

clc; clear all;
% Systemparameter
m1 = 20;         %Radmasse /kg
m2 = 2000/4;     %Aufbaumasse /kg
m3 = 80/4;       %Fahrermasse /kg
c1 = 100000;     %Federsteifigkeit Rad /N/m
c2 = 20000;      %Federsteifigkeit Fahrwerk /N/m
c3 = 10000;      %Federsteifigkeit Sitz /N/m
k2 = 1400;       %Dämpfung Stoßdämpfer /Ns/m
k3 = 300;        %Dämpfung Sitz /Ns/m

tend=2;     %Simulationsdauer

%Systemmatrix
A = [       0       1      0        0     0    0;
    -(c2+c1)/m1  -k2/m1  c2/m1    k2/m1   0    0;
            0       0      0        1     0    0;
          c2/m2   k2/m2 -(c3+c2)/m2 -(k3+k2)/m2  c3/m2  k3/m2;
   0    0    0       0        0        1;
   0    0  c3/m3   k3/m3   -c3/m3   -k3/m3];

%Steuermatrix
B = [0 c1/m1 0 0 0 0]';

%Beobachtungsmatrix
C = [1 0 0 0 0 0];   % Radbewegung wird beobachtet

%Durchgriffsmatrix
D = [0];

%Zeitbasis
t=0:0.001:tend;

%Eigenfrequenzen
fRad    =round(100*sqrt((c1+c2)/m1)/(2*pi))/100
fAufbau =round(100*sqrt(c2/m2)/(2*pi))/100
fFahrer =round(100*sqrt(c3/m3)/(2*pi))/100

% Straße
    f=fRad;                                      %Anregungsfrequenz
    h=cos(f*t*2*pi)*0.2-0.2;                     %Sinusanregung
    %h=[zeros(40,1); 0.2*ones(length(t)-40,1)]'; %Kante
    %h=rand(1,length(t))*0.2;                    %stochastische Anregung

% Berechnung
system = ss(A,B,C,D);       %Definition des Zustandsraummodells
[y,t,x]=lsim(system,h,t);   %Simulation

Durch die Berechnung lsim wird nun die Trajektorie des Zustandsvektors für jeden diskreten Zeitschritt t berechnet. Die interessanten Größen sind die Auslenkungen von Rad, Aufbau und Fahrer. Diese sind im Zustandsvektor x in der 1., 3. und 5. Zeile abgelegt. Da der Beobachtungsvektor c=[1 0 0 0 0 0] definiert wurde, ist der Systemausgang y der Radhub.

Radhub    = x(:,1);
Aufbauhub = x(:,3);
Fahrerhub = x(:,5);
plot(t, [h', Radhub, Aufbauhub, Fahrerhub]);
legend('Strasse','Rad','Aufbau','Fahrer');
xlabel('Zeit [s]');
ylabel('Vertikalbewegung [m]');

Simulationsergebnisse

Überfahren einer Bodenunebenheit

Anregung in kritischen Frequenzen

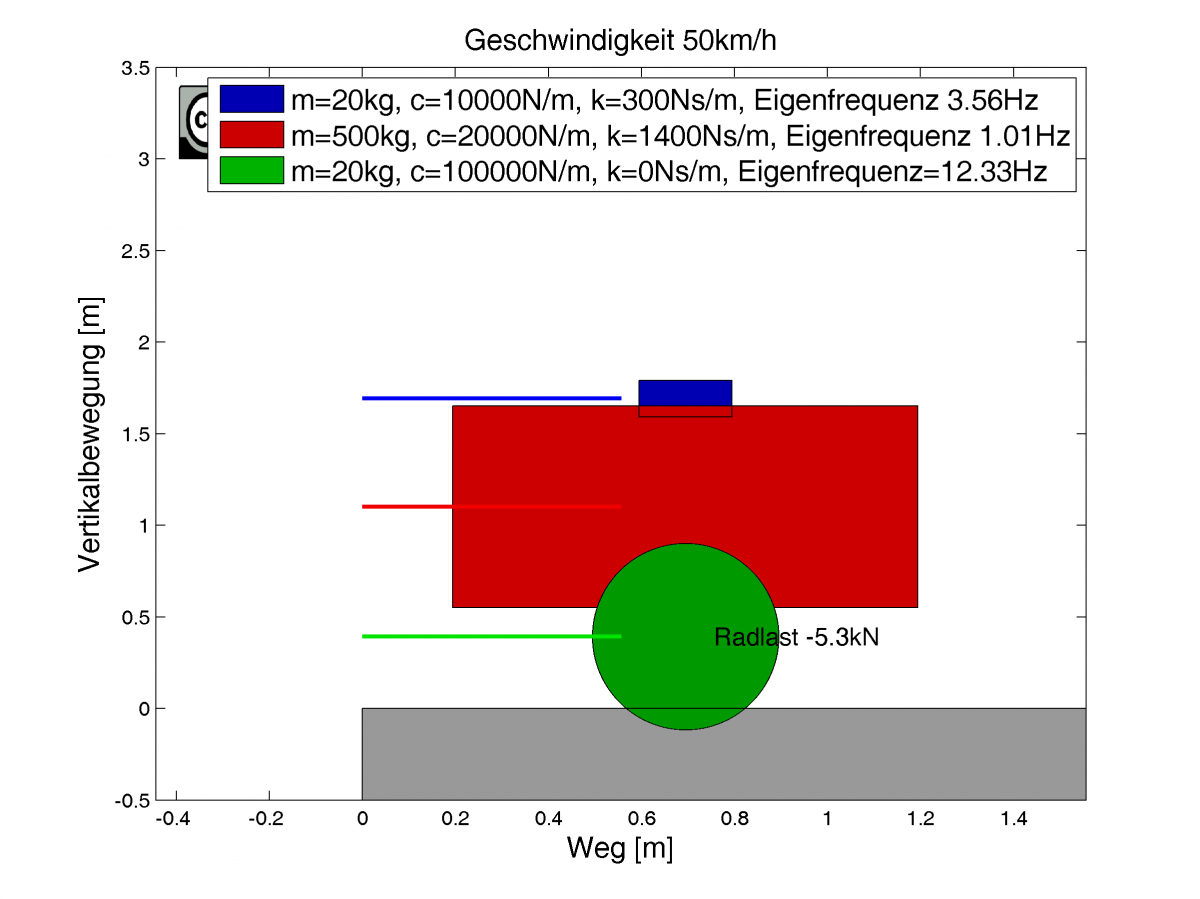
Interessant ist, dass berechnet werden kann, in welchem Bereich die Eigenfrequenzen von Aufbau, Rad oder Fahrer liegen. Diese sind für die gewählten Parameter bei ca. 1Hz (Aufbau), 3Hz (Fahrer) und 12Hz (Rad).

Die Berechnung ist natürlich so vereinfacht, dass keine geometrischen Beschränkungen (Rad ist vollständig Ein-/Ausgefedert oder Aufbau schlägt auf Straße auf) implementiert sind. Grundsätzlich ist die Animation einer fahrenden Bewegung auch nur zum besseren Verständnis erstellt worden.

Weitere Animationen

Zweimassenschwinger in Excel

Wer die Schwingung in Excel ansehen möchte, der kann sich auch folgende Excel Datei runterladen:

  Download Excel Viertelfahrzeug Schwingung

In dieser wurde einfach die Differentialgleichung numerisch integriert.