Ein Thema, was mich schon lange beschäftigt, was aber wahrscheinlich die wenigsten Menschen überhaupt interessieren dürfte, möchte ich in diesem Beitrag mal abhandeln. Es geht dabei um das Differenzieren verrauschter Signale. Da stellt sich natürlich die Frage: Wo kommt so etwas überhaupt vor? An unglaublich vielen Stellen kommt das vor. Immer wenn man von einer gemessenen Größe auf eine andere schließen möchte, welche differenziellen Zusammenhang hat. Beispielsweise bei der Leistungsmessung auf einem Rollenleistungsprüfstand oder wenn man aus Positionsangaben einer GPS Messung die Geschwindigkeit berechnen möchte oder oder oder.

Differenzieller Zusammenhang am Beispiel der Leistungsmessung am Rollenleistungsprüfstand
Am Beispiel der Leistungsmessung auf einem Rollenleistungsprüfstand kann man sich das “Problem” sehr anschaulich darstellen. In diesem Beispiel wird die Leistungsmessung eines elektrischen Krads genutzt. Die Größe, welche vom Prüfstand gemessen wird, ist die Drehzahl der Rolle. Die Größe, welche für die Drehmomentberechnung benötigt wird, ist die Winkelbeschleunigung α. Zwischen Drehzahl n und Winkelbeschleunigung α gibt es einen differentiellen Zusammenhang.
Das funktioniert alles super, so lange man das analytisch machen kann, also “den Anstieg an der Funktion berechnen”. Im realen Leben hat man aber fast nie eine Funktion gegeben, sondern die Drehzahl kommt von einem Sensor, welcher zum einen normalverteilte Messfehler hat, zum anderen nur mit endlicher Auflösung vom Mikrocontroller oder PC eingelesen werden kann. Am Beispiel der Leistungsmessung sieht die ermittelte Drehzahl beispielsweise so aus.
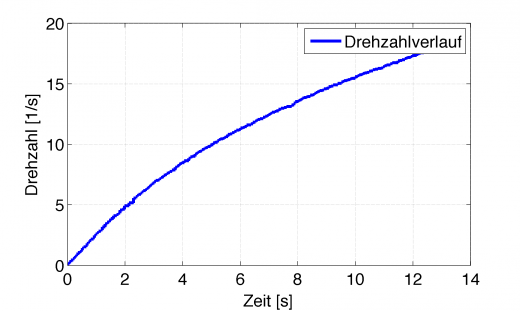
Das sieht ja auf den ersten Blick ganz gut aus. Eine schön saubere Kurve, welche die gemessene Drehzahl da erzeugt. Doch im Allgemeinen steht dafür kein analytischer Ausdruck zur Verfügung, den man ableiten kann sondern man muss den Euler-Cauchy Ansatz wählen und das Differential einfach durch eine Differenz ersetzen.
Wobei die Differenz einfach zum vorherigen Wert gebildet wird. Ist der Zeitschritt Δt nur klein genug, geht das mathematisch sauber durch. Es wird also die Drehzahländerung pro Zeitänderung berechnet.
Wo ist das Problem?
Am einfachsten kann man es sich vorstellen, wenn man die Drehzahl nur mit 1bit aufgelöst digitalisiert (es gibt nur 0 Umdrehungen/s und 15U/s als Werte), aber mit 1MHz abtastet. Dann ist die Winkelbeschleunigung nach Euler-Cauchy Ansatz:
Diese gigantische Winkelbeschleunigung gilt aber nur in diesem einen Abtastschritt, an dem das Signal von 0U/s auf 15U/s springt. Sonst ist die diskrete Differentiation 0.
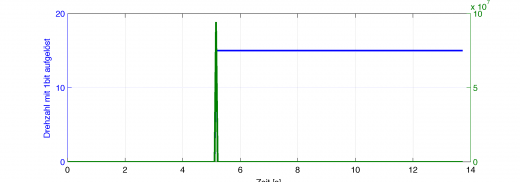
blau: Eine mit 1bit aufgelöste Drehzahl (springt bei reichlich 5s von 0 auf 15U/s)
grün: Numerische Differentiation dieser Drehzahl mit Δt=1μs.
Mit diesem Signal kann man offensichtlich nichts anfangen. Ganz so dramatisch ist es nicht, aber auch bei 8bit oder 16bit Auflösung ergeben sich diese Zusammenhänge.
Differentiation mittels explizitem Euler-Verfahren
Der Matlab Code für diese numerische einseitige Differentiation ist folgender:
%% Euler-Cauchy-Ansatz zur numerischen Differentiation % Matlabs ''diff'' Funktion berechnet nur einseitige Differenzen % Das heißt, dass nur zum nachfolgenden Punkt eine Differenz vom aktuellen % aus berechnet wird alpha = diff(omega)./diff(t); alpha = [0; alpha];
Für das Beispiel der Drehzahlmessung ergibt sich folgende Differentiation mittels explizitem Euler-Verfahren:
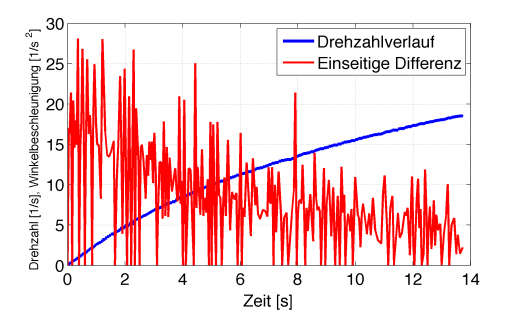
Numerische Differentiation einer verrauschten Messgröße (blau) mittels einseitigem Differential (rot)
Das ist nicht falsch, das ist einfach nur kaum brauchbar. Sieht man sich das Übertragungsverhalten eines idealen Differenzierers an, so wird deutlich, dass dieser extrem die hohen Frequenzanteile verstärkt. Mit dieser extrem verrauschten Winkelbeschleunigung berechnet man jetzt aber leider das Drehmoment.
Es kann sich jeder vorstellen, dass dieses rote Signal multipliziert mit einem Massenträgheitsmoment J dann einen ähnlichen Verlauf ergibt. Das wäre die fertige Drehmomentkurve, wie sie ohne weiteres von so einem Rollenleistungsprüfstand berechnet werden könnte. Sofort wird der Ruf nach Filterung laut.
Filterung
Der einfachste ist der Mittelwertfilter. Sagen wir, man mittelt das differenzierte Signal über 50 Werte. Der Matlab Code dazu ist folgender:
%% Gefilterte Beschleunigung mit Mittelwertfilter über 50 fl=50; alphaf = filter(ones(1,fl)/fl,1,alpha); plot(t,alphaf,'k','Linewidth',2)
Es ergibt sich folgender gefilterter Verlauf.
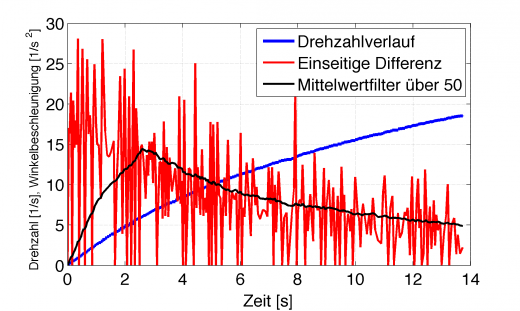
Differenziertes Signal mit Mittelwertfilter über 50 Werte (schwarz)
Das ist zwar etwas ansehnlicher, aber nicht mehr korrekt. Der Mittelwertfilter kann natürlich erst den ersten richtigen Mittelwert ausgeben, nachdem 50 Werte zur Berechnung vorlagen. Klar, dass umso höher der Grad der Filterung wird, das Ergebnis auch immer falscher und vor allem zeitversetzter wird. Der Extremfall wäre ja, wenn man über alle vorliegenden Werte filtert, dann hat man nur noch einen einzigen Mittelwert am Ende der Messung. Man kann sich praktisch jeden Drehmomentverlauf hinrechnen, den man haben möchte, nur durch die Wahl des Filtergrades. Ein Beispiel: Die Leistung des Fahrzeugs wird berechnet über
Somit ergeben sich, je nach Filtergrad des Mittelwertfilters, folgende Leistungsverläufe aus der Drehzahlmessung, wenn man für J=5kgm² annimmt:
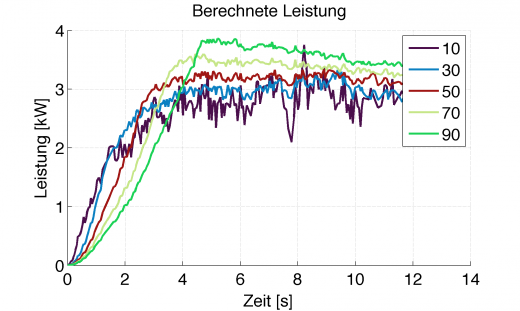
Berechnete Leistung aus gefiltertem Drehwinkelbeschleunigungsverlauf, Farben stellen Grad der Filterung dar
Das ist wohl jedem klar, dass zwischen den verschiedenen Kurvenverläufen im realen Fahrverhalten Welten liegen. Was also tun?
Zentrales Differential
Besser als das einseitige Differential ist das zentrale Differential. Der Prof. Jörn Loviscach erklärt das recht anschaulich:
Der Matlab Code dazu ist folgender:
%% Besser ist mit zentralen Differenzen zu arbeiten % Dabei wird der Anstieg im Punkt nur aus der Differenz zwischen dem % vorherigen und dem nachfolgenden berechnet, nicht aus dem Punkt selbst i=length(n); alphacentral = (omega(3:i)-omega(1:i-2))./(t(3:i)-t(1:i-2)); alphacentral = [0;alphacentral;0];
Damit hat man immer noch kein extrem besseres Ergebnis, allerdings ist man schon dichter an der Wahrheit dran.
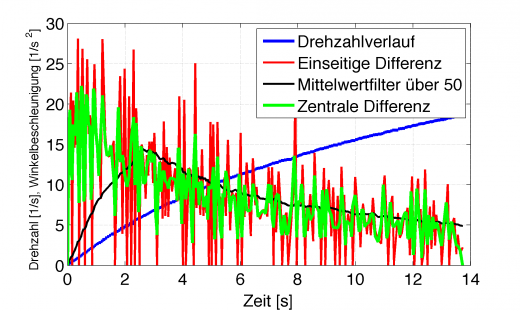
Auch in diesem Verlauf ist deutlich der Hochpasscharakter erkennbar, der Verlauf ist aber schon ruhiger als mit einseitigem Differential. Richtig gut zu verwenden allerdings immer noch nicht.
Man merkt offensichtlich, dass das nicht so einfach ist.
OK, dann eben nicht simply
Es gibt weitere Varianten, wie man trotzdem mit verrauschten Daten eine numerische Differentiation hinbekommt. Zum einen könnte man die gemessenen Daten vorher entsprechend filtern. Zum anderen kann man eine lokale polynomische Regression vornehmen, welche dann differenziert wird. Die Ausgabe des differenzierten Werts kann dann zwar nicht mehr in Echtzeit erfolgen, aber 1-2ms kann man oftmals auch “warten”, vor allem wenn es nur um die Anzeige der Kurven geht.
Das Savitzky–Golay Filter
Ein gutes Beispiel dafür ist das FIR Filter nach Savitzky und Golay. Bei diesem wird, je nach Fenstergröße, lokal ein Polynom durch die verrauschten Messwerte gelegt und dieses dann numerisch differenziert. Die Koeffizienten für die Polynome können im englischsprachigen Wikipedia Eintrag zum Savitzky-Golay Smoothing nachgelesen werden. Dies sogar direkt für die 1. und 2. Ableitung.
Die Matlab Implementierung für das Savitzky-Golay Filter ist:
%% Savitzky-Golay Smoothing filter
% Polynom 2. Grades mit Fenstergröße 9 für 1st Ableitung
dt=mean(diff(t)); % konstante Abtastrate angenommen
alphasg=1/60.*1./dt.*(...
-4*omega(1:i-8)...
-3*omega(2:i-7)...
-2*omega(3:i-6)...
-1*omega(4:i-5)...
+1*omega(6:i-3)...
+2*omega(7:i-2)...
+3*omega(8:i-1)...
+4*omega(9:i));
alphasg=[0;0;0;0;alphasg;0;0;0;0];
Man kann für eine Fensterbreite von 9 erst ab dem 5. Wert ein Ergebnis bekommen, die letzten 4 sind ebenfalls wieder 0. Daher der merkwürdige Verlauf zu Beginn und am Ende.
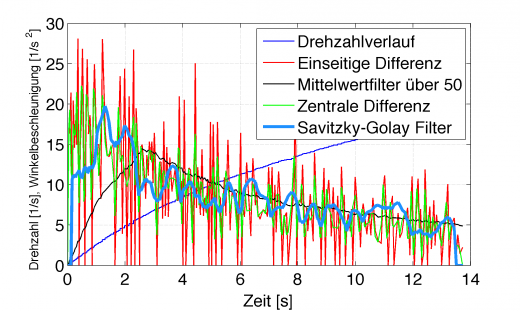
Richtig schön ist das immer noch nicht, aber wie Prof. Buchholz dazu sagte:
In der Praxis klappt das Differenzieren verrauschter Signale eigentlich nie.
Du verletzt dabei das GIGO (Garbage In, Garbage Out)- Theorem.
Mögliche Lösung: Vorab Modellieren
An den Grundprinzipien, nämlich dem Hochpasscharakter eines Differenzierers und dem Phasenverzug beim Filtern kann selbst das beste Filter nichts ändern! Es wird immer mittelmäßig bleiben. Falls es also nicht unbedingt auf eine Echtzeitanwendung bzw. -berechnung hinaus läuft und man “nur” ein Diagramm benötigt, so bietet es sich an vor dem Differenzieren eine Filterung vorzunehmen. Noch idealer, wenn man eine analytische Beschreibung der ursprünglichen Daten finden kann. An dem hier vorgestellten Beispiel wäre das z.B. ein Polynom, welches den Drehzahlverlauf optimal beschreibt.
Mit der Methode der kleinsten Quadrate kann man ein beliebiges Modell zu den Daten angepasst finden, welches optimal dazu passt. Der Matlab Code zur Berechnung eines Polynom 3. Grades lautet:
%% Polynomial Fit der ursprünglichen Daten % Modellannahme ist Polynom 3. Grades N = [ones(length(t),1),t,t.^2,t.^3]; p = N\n % Least-Square-Fit der Daten npol = N*p; % modellierte Drehzahl
Das kubische Polynom passt offensichtlich bestens zu dem Drehzahlverlauf:
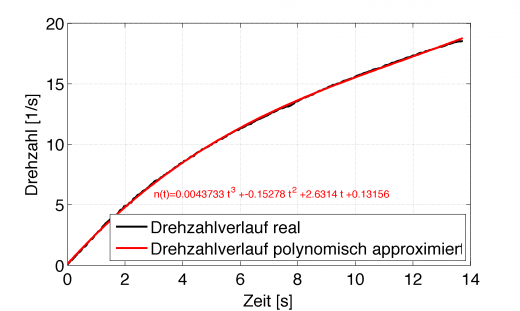
Diese Funktion kann man dann auch wieder analytisch ableiten und erhält für die Winkelbeschleunigung ebenfalls eine analytische Gleichung, welche dann zum jeweiligen Zeitpunkt mit dem Massenträgheitsmoment multipliziert das Drehmoment ergibt.
Stellt man diese berechneten Werte nun über der Drehzahl dar, so ergibt sich das wohl ansehnlichste Diagramm dieses Schauspiels:
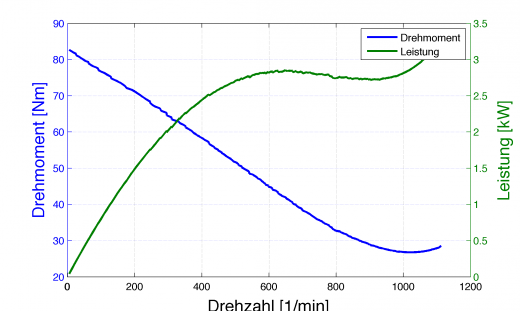
Gut zu erkennen ist hier der Fehler der Modellannahme (Approximation der Drehzahl durch das Polynom), denn im Bereich >1000U/min steigt das Drehmoment wieder an, was eigentlich keinen Sinn macht. Es ist Zeit die Modellannahme nochmals zu überprüfen und eventuell andere Approximationen als ein Polynom zu wählen. Doch das ist ein anderes Thema, womit man sich mal beschäftigen kann.
Dieser Beitrag entstand mit freundlicher Unterstützung von Prof. Jörn Loviscach und Prof. Jörg Buchholz






6 Comments
Hallo,
das sind sehr interessante Ansätze.
In Ergänzung zum letzten Teil möchte ich betonen, dass man sich aus der Anwendung heraus ein *sinnvolles* Modell überlegen sollte anstatt einfach ein Polynom zu nehmen. Insbesondere sollte man von Polynomen hohen Grades die Finger lassen. Sie mögen nah an den Datenpunkten liegen, neigen aber zwischen den Datenpunkten zu Oszillationen und streben außerhalb der Datenpunkte schnell gegen unendlich.
Im Beispiel bietet sich auf den ersten Blick ein Ansatz der Form
y = a*exp(-b*t) + c*t + d
an, evtl. sogar ohne den linearen Term.
Grüße,
Harald
Hat mir sehr geholfen, vielen Dank
Hallo,
vielen Dank für den interessanten Artikel.
Es ist schon ein paar Jahre her, aber vielleicht liest ja doch jemand die Kommentare.
Ich bin in meiner Bachelorarbeit auf genau dieses Problem gestoßen. Liegt dem Artikel Literatur zugrunde, die man zitieren könnte?
Ich habe den Artikel nur kurz überflogen. Dennoch möchte ich ein paar generelle Dinge zur Signalverarbeitung anraten.
Eingangs wird erläutert, dass das Messsignal mit Störungen überlagert ist. Von diesem Messsignal soll die zeitliche Ableitung gebildet werden. Es gehört zum inhärenten Wesen der Differentiation, dass sie, auf Signale angewendet, Störungen verstärkt. Daraus lässt sich direkt eine erste Regel ableiten, die man in der Signalverarbeitung immer im Hinterkopf behalten sollte:
Regel 1: In der Regel sollten gestörte Signale zunächst entstört werden (bspw. durch Filterung), bevor es an die weitere Signalverarbeitung geht.
Hier heißt das konkret:
Nicht die Ableitung bilden und dann versuchen diese Ableitung irgendwie zu “säubern”. Auch nicht mit irgendwelchen anderen Verfahren die Ableitung bilden (hier vorgeschlagen das zentrale Differential) und dann die so gewonnene Ableitung entstören.
Sondern: Erst das Messsignal “säubern” (z.B. Filterung) und erst dann die weiter Signalverarbeitung (hier Ableitung) vornehmen.
Zur Beseitigung von Störungen gibt es sehr viele Filter, die alle auf spezielle Störungen spezialisiert sind. So kann man beispielsweise Spikes zwar mit einem Tiefpass zu Leibe rücken, aber das Ergebnis wird sehr mittelprächtig sein. Und hochfrequentes Rauschen mit einem Median-Filter zu beseitigen liefert auch keine guten Ergebnisse.
Im hier genannten Beispiel wird von normalverteilten Messfehlern ausgegangen (die vermutlich zusätzlich noch mindestens von thermischen Rauschen überlagert sind). Die erste Wahl zum Filtern fällt leider viel zu oft auf die gleitende Mittelwertbildung. Für diese gilt aber
Regel 2: In der überwiegenden Mehrheit aller Fälle ist eine gleitende Mittelwertbildung eine äußerst _schlechte_ Filtermethode, denn (stichwortartig und nur eine kleine Auswahl der Nachteile):
* Sie hat eine äußerst mäßige Dämpfung im Sperrbereich (selbst bei großen N sind die Störungen noch deutlich sichtbar, siehe die Diagramme oben).
* Sie hat eine große Einschwingzeit (sehr schön in den Diagrammen oben zu sehen).
* In einer Echtzeitanwendung hat sie auch noch eine (sehr) große Signalverzögerung.
Interessant ist, wie oft der Savitzky-Golay Filter Erwähnung findet. Aber selbst Matlab scheint nicht genügend deutlich herauszustellen, wofür der Savitzky-Golay Filter entwickelt worden ist und wofür er daher eher wenig geeignet ist.
Regel 3: Der Savitzky-Golay-Filter ist eine Polynomglättung, die zwar eine Tiefpass-Charakteristik hat. Er ist aber für die Glättung von verrauschten Spektren entwickelt worden, bei der hohe Spektralanteile nicht einfach abgeschnitten werden dürfen. Damit ist der Savitzky-Golay-Filter zur Filterung von verrauschten Signalen i.d.R. wenig brauchbar.
Wie also dann verrauschte Messsignale behandeln?
Regel 4: Bei verrauschten Signalen sollte zunächst immer der Einsatz eines Tiefpassfilter (IIR, ggf. auch FIR)) erwogen werden. Nur bei Signalen mit extrem steilen Flanken (bspw. verrauschte Rechtecksignale) stoßen diese Filter an Grenzen.
Bei den IIR gibt es leider wieder eine Auswahl verschiedener Filter (die häufigsten: Butterworth, Chebyshev, Invers-Chebyshev, Elliptisch), die alle ihre Stärken und Schwächen haben, auf die ich hier nicht weiter eingehen kann.
Aber wenn man so vorgeht – Messsignal mit Butterworth filtern, dann normales Differential anwenden – bekommt man eine absolut glatte Ableitung. Leider kann ich hier kein Bild hochladen, um dies zu zeigen ☹.
Ich hoffe dass dieser recht ausführliche Kommentar dem ein oder anderen ein wenig helfen mag.
Can you provide examples of applications or industries where real-time processing is critical, and how practitioners balance the need for real-time results with the challenges posed by noisy data?