[Tutorial] Rotationsmatrix und Quaternion einfach erklärt in DIN70000 ZYX Konvention

Die Rotation eines Körpers im Raum ist ein Thema, welches einen Ingenieur in vielen Einsatzbereichen tangiert. Es gibt auch schon unzählige Webseiten dazu und auch die Wikipedia lässt sich zum Thema Drehmatrix oder Eulersche-Winkel ausführlich aus.

Doch so richtig gepasst hat bisher keine Beschreibung. Deshalb an dieser Stelle noch einmal eine ausführliche und einfache Beschreibung der 3D Rotation eines Körpers/Vektors mit Euler-Winkeln nach ZYX-Konvention im DIN70000 Koordinatensystem des Fahrzeugs.

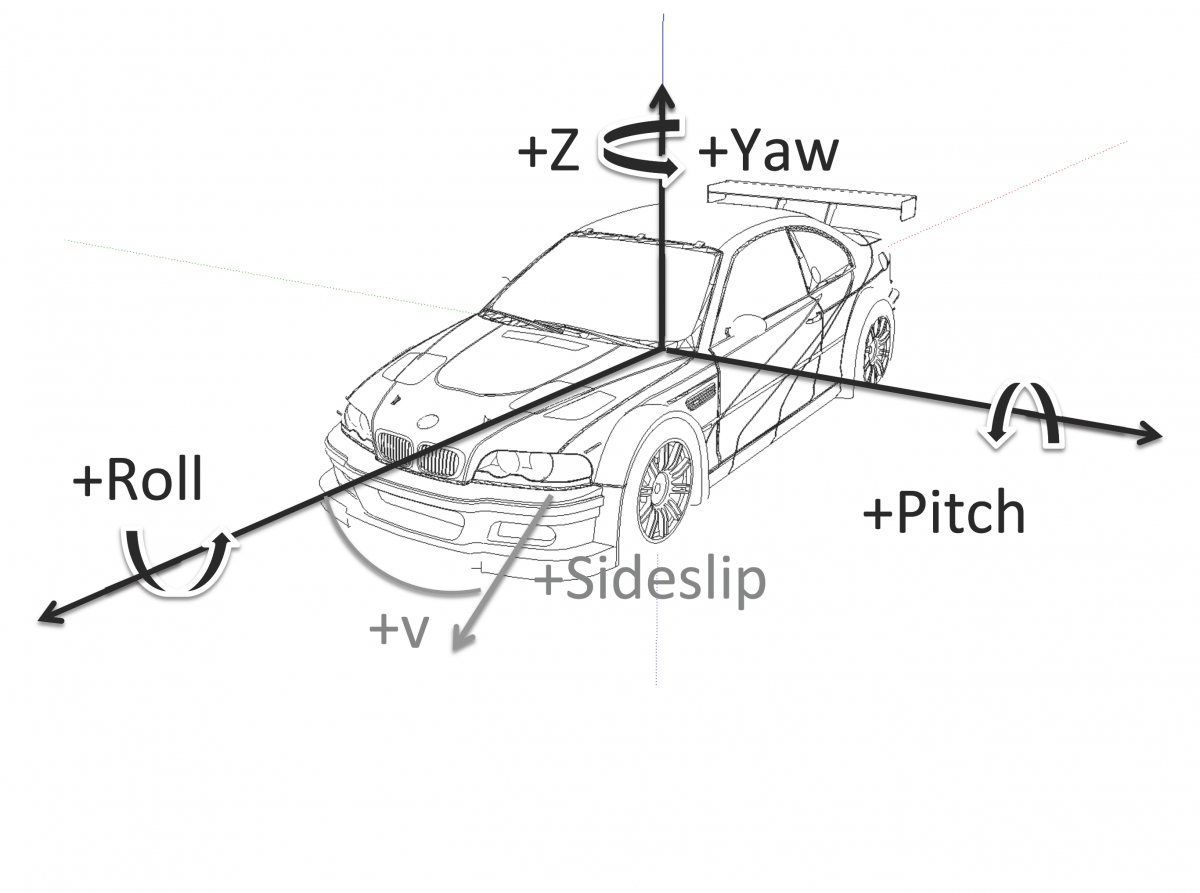
Das Koordinatensystem ist folgendermaßen definiert:

• x-Achse in Fahrzeuglängsrichtung positiv
• y-Achse nach links positiv
• z-Achse nach oben positiv
• Drehungen um die Achsen mit rechter Hand Regel positiv (Daumen zeigt in Richtung der Achse, Finger zeigen positive Drehrichtung)

Die Drehung ist nach ZYX Konvention folgendermaßen definiert:

• um Z-Achse, welche die Gierachse ([engl.: Yaw]) ist, bei Linkskurve positiv
• um Y-Achse, welche die Nickachse ([engl.: Pitch]) ist, beim Eintauchen der Fahrzeugfront positiv
• um X-Achse, welche die Rollachse ([engl.: Roll]) ist, beim Eintauchen der Beifahrerseite positiv

Natürlich kann man das beliebig anders definieren, aber dann muss man sich eben über die Rotationsmatrix und die Quaternion wieder selbst Gedanken machen. Behält man die Definition bei, so kann die Drehung einfach mit nachfolgenden Berechnungen vollführt werden.

Rotationsmatrix für ZYX Konvention berechnen

Die Rotationsmatrix setzt sich zusammen aus 3 einzelnen Matrizen, jeweils für Z-Rotation, Y-Rotation und X-Rotation:

$$\begin{align}
R & =
\begin{pmatrix}
1 & 0 & 0 \\
0 & \cos \phi & -\sin \phi \\
0 & \sin \phi & \cos \phi
\end{pmatrix}
\begin{pmatrix}
\cos \theta & 0 & \sin \theta \\
0 & 1 & 0 \\
-\sin \theta & 0 & \cos \theta
\end{pmatrix}
\begin{pmatrix}
\cos \psi & -\sin \psi & 0 \\
\sin \psi & \cos \psi & 0 \\
0 & 0 & 1
\end{pmatrix}
\end{align}$$

mit \(\psi = \textrm{Gieren}\), \(\theta = \textrm{Nicken}\), \(\phi = \textrm{Wanken}\) (von rechts multiplizieren)

Die ausmultiplizierte Version wird hier nicht angegeben.

Python Implementierung für Rotationsmatrix nach ZYX Konvention

def Rypr(y, p, r):
    '''
    Rotationsmatrix für y=yaw, p=pitch, r=roll in degrees
    '''
    # from Degree to Radians
    y = y*np.pi/180.0
    p = p*np.pi/180.0
    r = r*np.pi/180.0

    Rr = np.matrix([[1.0, 0.0, 0.0],[0.0, np.cos(r), -np.sin(r)],[0.0, np.sin(r), np.cos(r)]])
    Rp = np.matrix([[np.cos(p), 0.0, np.sin(p)],[0.0, 1.0, 0.0],[-np.sin(p), 0.0, np.cos(p)]])
    Ry = np.matrix([[np.cos(y), -np.sin(y), 0.0],[np.sin(y), np.cos(y), 0.0],[0.0, 0.0, 1.0]])

    return Ry*Rp*Rr

Die Rotationsmatrix erhält man durch Aufrufen der Funktion mit den 3 Rotationswinkeln als Argument:

R = Rypr(gieren, nicken, wanken)

Anschließend kann man einen beliebigen Vektor (oder Koordinatensystem oder Körper) mit der Rotationsmatrix multiplizieren und erhält das gedrehte Pendant. Sie ist z.B. geeignet, um ein erdfestes Koordinatensystem in das Fahrzeug-Koordinatensytem zu transformieren.

Beispielhaft ein Vektor \(g=\begin{bmatrix}1 & 0 & 0\end{bmatrix}^T\), welcher in positive x-Richtung zeigt, um 60 Grad um die Z-Achse gedreht und 45 Grad um die Y-Achse geneigt:

Die Rücktransformation des gedrehten Vektors kann mit der transponierten Rotationsmatrix erfolgen.

Problem des Gimbal-Lock bei Euler Drehung

Das Problem an der Drehung mit 3 Winkeln besteht dann, wenn eine solche Konfiguration entsteht, bei welcher 2 Drehachsen übereinander liegen.

Bei der ZYX-Konvention, wird der Gimbal-Lock erreicht, wenn der Nickwinkel \(\theta=90^\circ\) eingestellt wird. Dann ist sowohl Rollen als auch Gieren die gleiche Bewegung, welche allerdings keine Änderung der Lage mehr hervorruft. Dieser Zustand ist das so genannte “Gimbal-Lock” und muss verhindert werden.

Aus diesem Grund wird häufig die Rotation mit der Quaternion vorgezogen.

Rotation mit Quaternion

Die Quaternion ist eine Erweiterung der komplexen Zahlen. Im Grunde genommen nur ein theoretisches Konstrukt, welches es ermöglicht, solche Berechnungen anzustellen.

Ähnlich wie bei den komplexen Zahlen, die als Summe aus Real- und Imaginärteil beschrieben werden (\(Z = a\cdot 1 + b \cdot \mathrm{i}\)), wird die Quaternion als Linearkombination aus 3 Imaginärteilen und einem Realteil konstruiert:

\(q = \underbrace{a\cdot 1}_{\textrm{real}} + \underbrace{b \cdot \mathrm{i} + c \cdot \mathrm{j} + d \cdot \mathrm{k}}_{\textrm{imag}}\)

Bei der Beschreibung der 3D-Drehung mit der Quaternion, wird mit den imaginären Elementen b, c und d ein Vektor definiert, um den (mit a) gedreht wird.

Dabei berechnet sich der Drehwinkel

\(w=2\arccos(a)\)

und die 3 Vektorkoordinaten der Rotationsachse:

\(n_R=\left[\begin{matrix}\cfrac{b}{\sin(\frac{w}{2})} \\ \cfrac{c}{\sin(\frac{w}{2})} \\ \cfrac{d}{\sin(\frac{w}{2})}\end{matrix}\right]\)

Dabei ist die Rotation nur mit der Einheitsquaternion möglich. Die folgende Funktion normiert die Quaternion auf die Einheitsquaternion:

def normQ(q):
    '''Calculates the normalized Quaternion
    a is the real part
    b, c, d are the complex elements'''
    # Source: Buchholz, J. J. (2013). Vorlesungsmanuskript Regelungstechnik und Flugregler.
    # GRIN Verlag. Retrieved from http://www.grin.com/de/e-book/82818/regelungstechnik-und-flugregler
    a, b, c, d = q

    # Betrag
    Z = np.sqrt(a**2+b**2+c**2+d**2)

    return np.array([a/Z,b/Z,c/Z,d/Z])

Rotationsmatrix aus Quaternion

Die Rotationsmatrix kann aus der Quaternion berechnet werden, falls sie benötigt wird.

$$R = \left[\begin{matrix}(a^2+b^2-c^2-d^2) & 2(bc-ad) & 2(bd+ac) \\ 2(bc+ad) & (a^2-b^2+c^2-d^2) & 2(cd-ab) \\ 2(bd-ac) & 2(cd+ab) & (a^2-b^2-c^2+d^2)\end{matrix}\right]$$

Python Implementierung zur Berechnung der Rotationsmatrix aus der Quaternion

def QtoR(q):
    '''Calculates the Rotation Matrix from Quaternion
    a is the real part
    b, c, d are the complex elements'''
    # Source: Buchholz, J. J. (2013). Vorlesungsmanuskript Regelungstechnik und Flugregler.
    # GRIN Verlag. Retrieved from http://www.grin.com/de/e-book/82818/regelungstechnik-und-flugregler
    q = normQ(q)

    a, b, c, d = q

    R11 = (a**2+b**2-c**2-d**2)
    R12 = 2.0*(b*c-a*d)
    R13 = 2.0*(b*d+a*c)

    R21 = 2.0*(b*c+a*d)
    R22 = a**2-b**2+c**2-d**2
    R23 = 2.0*(c*d-a*b)

    R31 = 2.0*(b*d-a*c)
    R32 = 2.0*(c*d+a*b)
    R33 = a**2-b**2-c**2+d**2

    return np.matrix([[R11, R12, R13],[R21, R22, R23],[R31, R32, R33]])

Euler Winkel aus der Quaternion

Natürlich können auch die Euler-Winkel aus der Quaternion berechnet werden, falls benötigt.

$$\psi = \arctan\left(\cfrac{2(bc+ad)}{a^2+b^2-c^2-d^2}\right) \\
\theta = \arcsin(2(ac-bd)) \\
\phi = -\arctan\left(\cfrac{2(cd+ab)}{-(a^2-b^2-c^2+d^2)}\right)$$

Python Implementierung zur Berechnung der Euler Winkel aus der Quaternion

def Q2Eul(q):
    '''Calculates the Euler Angles from Quaternion
    a is the real part
    b, c, d are the complex elements'''
    # Source: Buchholz, J. J. (2013). Vorlesungsmanuskript Regelungstechnik und Flugregler.
    # GRIN Verlag. Retrieved from http://www.grin.com/de/e-book/82818/regelungstechnik-und-flugregler
    q = normQ(q)

    a, b, c, d = q

    gieren = np.arctan2(2.0*(b*c+a*d),(a**2+b**2-c**2-d**2)) * 180.0/np.pi
    nicken = np.arcsin(2.0*(a*c-b*d)) * 180.0/np.pi
    wanken = -np.arctan2(2.0*(c*d+a*b),-(a**2-b**2-c**2+d**2)) * 180.0/np.pi

    return np.array([gieren, nicken, wanken])

Die Rotation erfolgt nun mit der Quaternion genauso, wie mit Euler Winkeln. Einfach aus den Elementen a, b, c, d die Rotationsmatrix berechnen und den Vektor/Objekt rotieren.

Das nachfolgende Video zeigt dies anschaulich:

Video Tutorial zur Rotation mit Quaternion und Euler Winkel

Rotation einer Punktwolke

Natürlich kann auch eine Punktwolke rotiert werden und nicht nur ein Vektor. Das folgende Video zeigt das äquivalente Vorgehen. Die Software zur Simulation des Laserscanners (oder einer Kinect) ist BlenSor.

Das komplette IPython Notebook gibt es auf Github.