 Auf den Webseiten
Auf den Webseiten
kann man nach Anmeldung gegen verschiedene Leute weltweit Schach spielen. Das tue ich auch gelegentlich, sodass ich mir mal Gedanken über die Berechnung des Ratings (Punkte) gemacht habe.
Die Formel dazu steht in den FAQ und wird folgendermaßen beschrieben:
Players are rated using the following formula:
New Rating = Old Rating + K * (Score – Win Expectancy)
K is a constant (32 for 0-2099, 24 for 2100-2399, 16 for 2400 and above)
Score is 1 for a win, 0.5 for a draw and 0 for a loss.
The Win Expectancy is calculated using the following formula:
Win Expectancy = 1 / (10^((OpponentRating-YourRating)/400)+1)
Das ist zwar schön formuliert, sieht aber nicht sehr übersichtlich aus. Die Formel ist:
Dabei ist Score die entscheidende Größe:
Die Variable K sättigt die Punktevergabe für Spieler mit sehr hohen Ratings:
Gewinnwahrscheinlichkeit
Die Wahrscheinlichkeit ein Spiel zu gewinnen (WE) errechnet sich nach
Sieht immernoch etwas kompliziert aus, heißt aber folgendes:
Hat man einen Punktestand von 1200 und der Gegner gegen den man das Spiel gerade beendet (und es gilt der Punktestand zum Ende des Spiels, nicht zu Beginn!), hat einen Punktestand von 1600, so liegt die Gewinnwahrscheinlichkeit bei:
Damit ergibt sich das neue Rating bei einem Sieg zu
Würde man das Spiel mit einem Unentschieden beenden, hätte man immerhin noch 1213 Punkte, bei einer Niederlage wären es –3, also 1197.
Risiko
Ein Spieler mit einer hohen Punktzahl (z.B. 1600) geht also immer ein hohes Risiko ein, wenn er gegen einen Spieler mit geringerer Punktzahl (z.B. 1200) ans virtuelle Brett geht. Denn gewinnt er, bekommt er relativ wenig Punkte (+3), verliert er allerdings, geht es ans Eingemachte (-29).
Grafisch sieht das dann so aus, wenn man aus der Sicht eines 1200er Spielers rechnet:
Neues Rating nach Sieg, Niederlage oder Unentschieden
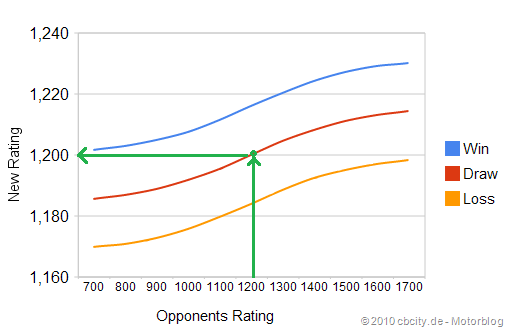
Spielt er gegen einen 1200er Spieler (Opponents Rating) und das Spiel geht unentschieden aus (Draw=rote Linie), so bleiben beide bei 1200 (New Rating).
Redhotpawn Rating Berechnung mit ScicosLab
Hier der Beispielcode zur Berechnung in SciLab:
clear; clf;
// Berechnung des RedHotPawn Ratings nach Sieg, Unentschieden
// oder Niederlage
my=1600; //Eigenes Rating
i=0; j=0;
for score=0:0.5:1 //Sieg;Unentschieden;Niederlage
j=j+1;i=0;
for his=800:1:2400 //Gegner zwischen 800...2400 Punkten
i=i+1;
x(i)=his;
K=32;
WE=1/(10^((his-my)/400)+1);
R(i,j)=round(my+K*(score-WE));
end
end
plot2d(x,[R(:,3),R(:,2),R(:,1)], [5, 2 3]);
legends([' Sieg';'Unentschieden';'Niederlage'],[5, 2 3],opt="lr");
xgrid(1);
xtitle('RedHotPawn.com Rating','Gegner Rating','Neues Rating')


