Motorblog » Alpha-Beta-Filter – der kleine Bruder vom Kalman Filter

Mit Abstand am häufigsten gelesen hier im Blog, sind die Beiträge zum Kalman Filter (Teil 1 & Teil 2 & EKF). In den Kommentaren und Emails, die ich dazu bekomme, zeigt sich allerdings, dass da mit Kanonen auf Spatzen geschossen wird. Einige Probleme, die der Algorithmus lösen soll, sind gar nicht so kompliziert, dass man einen Kalman Filter oder Extended Kalman Filter aufsetzen muss.

Ich möchte in diesem Beitrag den kleinen Bruder vom Kalman Filter, den Alpha-Beta-Filter, vorstellen. Dieser ist zwar im Grunde ein Kalman-Filter, allerdings mit einigen Vereinfachungen, sodass er leichter zu implementieren ist.

Fahrzeug-Tracking mit Alpha-Beta-Filter

Nehmen wir an, ein Fahrzeug fährt entlang einer Straße, man möchte die Position bestimmen. Dazu gibt es GPS Systeme, die periodisch (z.B. alle 1 Sekunde, im Folgenden wird ein Zeitschritt mit $k$ bezeichnet) die Position ermitteln. Die Positionsbestimmung durch GPS ist – wie alle Sensorwerte – fehlerbehaftet. Sie schwankt um den wahren Wert, der im Allgemeinen nicht bekannt ist.

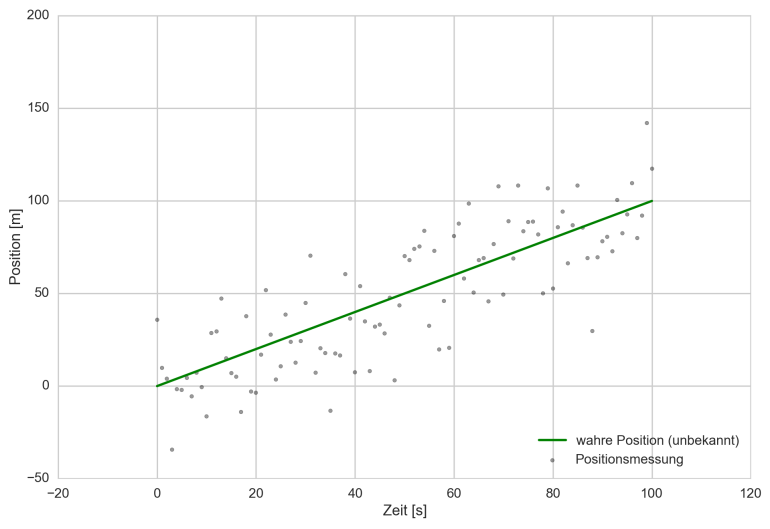
Wahre Position eines Fahrzeugs (grün) und durch GPS gemessene Position (grau)

Der große Vorteil des Alpha-Beta-Filters ist, dass dafür kein Systemmodell aufgebaut werden muss. Ist beim Kalman-Filter doch immer eine Dynamikmatrix mit der Systemdynamik aufzustellen, kommt der Alpha-Beta-Filter ohne eine solche aus. Es wird lediglich eine einfache mathematische Modellierung vorgenommen.

Es existiert ein Fahrzeug an einer beliebigen Position, z.B. bei $x=0$ , welches mit einer beliebigen Geschwindigkeit fährt. Beides ist zu Beginn festzulegen.

Dieses Fahrzeug, welches sich mit einer Geschwindigkeit $v$ bewegt, ist nach einer Zeit $\Delta T$ um $v \cdot \Delta T$ weiter gefahren. Dieser einfache Zusammenhang wird modelliert.

$x_k = x_{k-1} + \Delta T \cdot v_{k-1}$

Im nächsten Schritt wird die Geschwindigkeit gemessen oder einfach so gelassen, wie sie initialisiert wurde.

$v_k = v_{k-1}$

Residuum/Innovation

Nun wird bestimmt, wie gut die Modellierung zur tatsächlichen Messung passt.

$r_k = messung_k - x_k$

Dieses Residuum ist nun der entscheidende Teil, der die Innovation mit Hilfe der Faktoren Alpha und Beta aus macht.

Alpha

Der Faktor Alpha bestimmt, wie stark das Residuum sich auf das Update des Zustands auswirkt.

$x_k = x_k + \alpha \cdot r_k$

Beta

Der Faktor Beta bestimmt, wie stark die angenommene Geschwindigkeit geändert werden muss, um zur tatsächlichen Fahrzeugbewegung zu passen.

$v_k = v_k + \frac{\beta}{\Delta T}r_k$

Alpha-Beta-Tracking Filter Python Implementierung

Die Implementierung des Alpha-Beta Filters in Python sieht so aus:

x_k = 0.0
v_k = 1.0
dt = 1.0

alpha = 0.1
beta = 0.004

for k in range(len(messung)):
    x_k = x_k + dt*v_k
    v_k = 1.0
    r_k = messung[k] - x_k
    x_k = x_k + alpha*r_k
    v_k = v_k + (beta/dt)*r_k

Easy as that!

Wahl optimaler Alpha und Beta Faktoren

Die Frage ist natürlich, wie groß Alpha und Beta gewählt werden sollten. Das kann man pauschal nicht beantworten, denn es hängt immer davon ab, wie schnell sich der beobachtete Prozess ändern kann (in dem Fall: Wie schnell das Auto seine Geschwindigkeit ändern kann, d.h. wie hoch die Beschleunigung sein kann) und wie stark die Messwerte schwanken (in dem Fall: Wie gut das GPS die wahre Position misst). Im Sinne des Least-Square Ansatzes optimale Parameter können mit folgenden Formeln berechnet werden [Shimkin, N.: Kinematic Models for Target Tracking, Isreal Institute of Technology, Lecture Note, Fall 2009]:

Bestimmung der Unsicherheit der Annahme von konstanter Geschwindigkeit innerhalb eines Zeitschritts: $\sigma_w$
Bestimmung von Standardabweichung von GPS Messung $\sigma_v$

Dann

$\lambda = \cfrac{\sigma_w \Delta T^2}{\sigma_v}$

Lambda ist der so genannte ‘maneuvering index’, im Grunde das Verhältnis von Prozess-Rauschen (wie schnell kann das Auto seine Geschwindigkeit innerhalb eines Zeitschritts ändern?) und Mess-Rauschen (wie falsch kann das GPS messen?).

$\alpha_\text{opt} = \frac{1}{8}\left(-\lambda^2 - 8\lambda + (\lambda+4) \sqrt{\lambda^2+8\lambda}\right)$

$\beta_\text{opt} = \frac{1}{4}\left(\lambda^2 + 4\lambda -\lambda \sqrt{\lambda^2 + 8\lambda} \right)$

Die Python Implementierung sieht so aus:

sigma_v = np.var(messfehler)
sigma_w = 2.0*dt # 2m/s2 Beschleunigung
lamb = (sigma_w*dt**2.0) / sigma_v
alpha_opt = 1/8.0*(-lamb**2.0 - 8.0*lamb + (lamb+4)*np.sqrt(lamb**2.0 + 8.0*lamb))
beta_opt = 1/4.0*(lamb**2.0 + 4.0*lamb - lamb*np.sqrt(lamb**2.0 + 8.0*lamb))

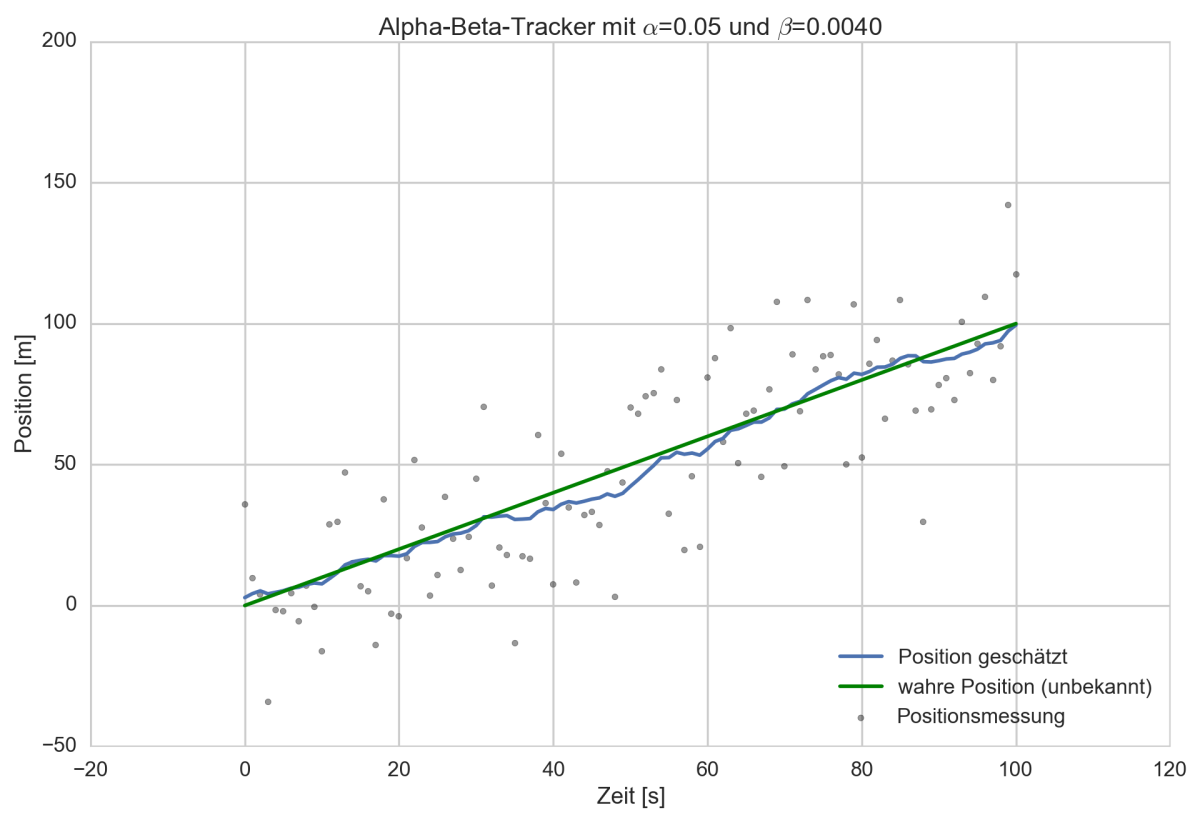
Tracking Ergebnis

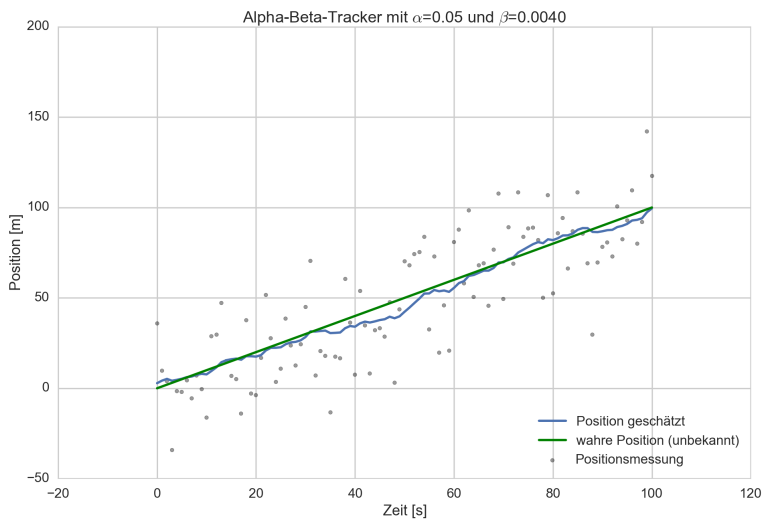
Wahre Fahrzeugposition (grün), gemessen durch GPS (graue Punkte) und durch Alpha-Beta-Filter geschätzt (blau)

IPython Notebook mit Code zum Alpha-Beta-Tracking

5 Comments

David sagt:

16. Februar 2016 um 19:49 Uhr

Hallo,

ich danke ihnen für diese tollen Ausführungen und Erklärungen!

Für den Alpha-Beta Filter nimmst du die GPS Position als Datenquelle an. Rechnest dann aber mit der Geschwindigkeit. Leitest du davür die Geschwindigkeit aus den GPS-Daten ab v = delta s / delta t.

Dann kann ich doch aber auch gleich schreiben
Xk = Xk-1 + delta s
Oder?

delta s = Position(k) – Position(k-1)

Antworten
1. Paul Balzer sagt:
  
  16. Februar 2016 um 20:01 Uhr
  
  Hey, danke!
  
  Nein, nicht ganz: Die Geschwindigkeit weißt du gar nicht, misst sie jedenfalls nicht. Sie ist ein “Systemzustand”, den du als Puffer lässt für eine ruhigere Bewegung. Du misst nur die Position (die ist verrauscht). Wenn sich etwas bewegt, dann muss es ja eine Geschwindigkeit haben. Das Alpha-Beta Filter geht von einer konstanten Geschwindigkeit aus.
  Nach ein paar Filterschritten ‘weiß’ das Filter (durch das Resisuum r) wie schnell das Auto fährt und kann damit die Bewegung glätten. Mit den Faktoren alpha und beta stellst du ein, wie schnell das Filter die Geschwindigkeit ‘lernt’ bzw. auf Geschwindigkeitsänderungen reagieren kann.
  Wenn du eine veränderliche Geschwindigkeit hast, dann kannst du auf einen Alpha-Beta-Gamma Filter upgraden, dann geht das Filter davon aus, dass die Längsbeschleunigung konstant bleibt.
  
  Hilft das?
  
  Antworten
  1. David sagt:
    
    17. Februar 2016 um 13:02 Uhr
    Ja,
    das Filter funkioniert echt gut.
    
    Bei deinem ersten Beispiel fehlt glaub ich noch die Initialisierung von v_k. Man könnte auch x_k auf den ersten Messwert legen. So muss der Filter noch von 0 starten.
    Im Loop wird v_k immer wieder auf 1 gesetzt. Ist das nötig? Nimmst du eine gleichmässige Geschwindigkeit von 1 an?
    
    Beispielprogramm für variable Geschwindigkeit und mit oder ohne zusätzlichens Speed Signal. Inputdaten kann sich sicher jeder selber erzeugen.
    
    Matlab Code :
    
    %p_messung = Verrauschte Positionsdaten [m] %v_messung = Gemessene Geschwindigkeit [m/s] dt = 0.01; %Zeit interval der Messung [s] x_k = p_messung(1); %Startposition v_k = 0; %Startgeschwindigkeit oder = v_messung(1); alpha = 0.04; beta = 0.001; position = []; %ermittelte Position for k = 1 : length(p_messung) x_k = x_k + dt*v_k; %v_k = v_messung(k); %wenn v_messung vorhanden sonst v_k=v_(k-1) r_k = p_messung(k) - x_k; x_k = x_k + alpha*r_k; v_k = v_k + (beta/dt) * r_k; position(k) = x_k; %Wert in Ausgabe Array speichern end figure('Color',[1 1 1]) hold on plot(p_messung,'Color','b'); plot(position,'Color','r');
  2. Paul Balzer sagt:
    
    17. Februar 2016 um 13:44 Uhr
    
    Danke! Fehler ist beseitigt. Dein Code funktioniert prima. Genau so!
Daniel sagt:

27. September 2017 um 15:27 Uhr

Hallo,

Vielen Dank für die Erklärungen und Auführungen!

Wie kann ich die optimalen Alpha-Beta-Gamma Faktoren bestimmen. Für einen Alpha-Beta Filter hat das wie von dir beschrieben sehr gut funktioniert. Aber wie geht das wenn Gamma noch dazu kommt…?

Antworten