Motorblog
Nachdem wir im Teil 1 den Kern des Kalman Filters geklärt haben, widmen wir uns nun dem komplizierteren Teil. Die im Teil 1 genannte Vorgehensweise mit dem multiplizieren bzw. addieren der Mittelwerte und Varianzen funktioniert so nur im eindimensionalen Fall. \(\)
Das heißt, wenn der Zustand, den man messen möchte, mit nur einer Variablen vollständig beschrieben werden kann. Das Beispiel, welches eingangs genannt wurde, die Position eines Fahrzeugs im Tunnel zu bestimmen, kann aber nicht mehr mit einer Variablen vollständig beschrieben werden. Zwar interessiert nur die Position, aber diese ist genau genommen ja schon 2-Dimensional in der Ebene (\(x\) & \(y\)). Außerdem kann nur die Geschwindigkeit (\(\dot x\) & \(\dot y\)) gemessen werden, nicht die Position direkt. Dies führt zu einem 4D-Kalman-Filter, mit folgenden Zustandsvariablen:
$$x=\begin{bmatrix}
x \\
y \\
\dot x \\
\dot y
\end{bmatrix}=\begin{matrix}\text{Position X} \\ \text{Position Y} \\ \text{Geschwindigkeit in X} \\ \text{Geschwindigkeit in Y}
\end{matrix}$$
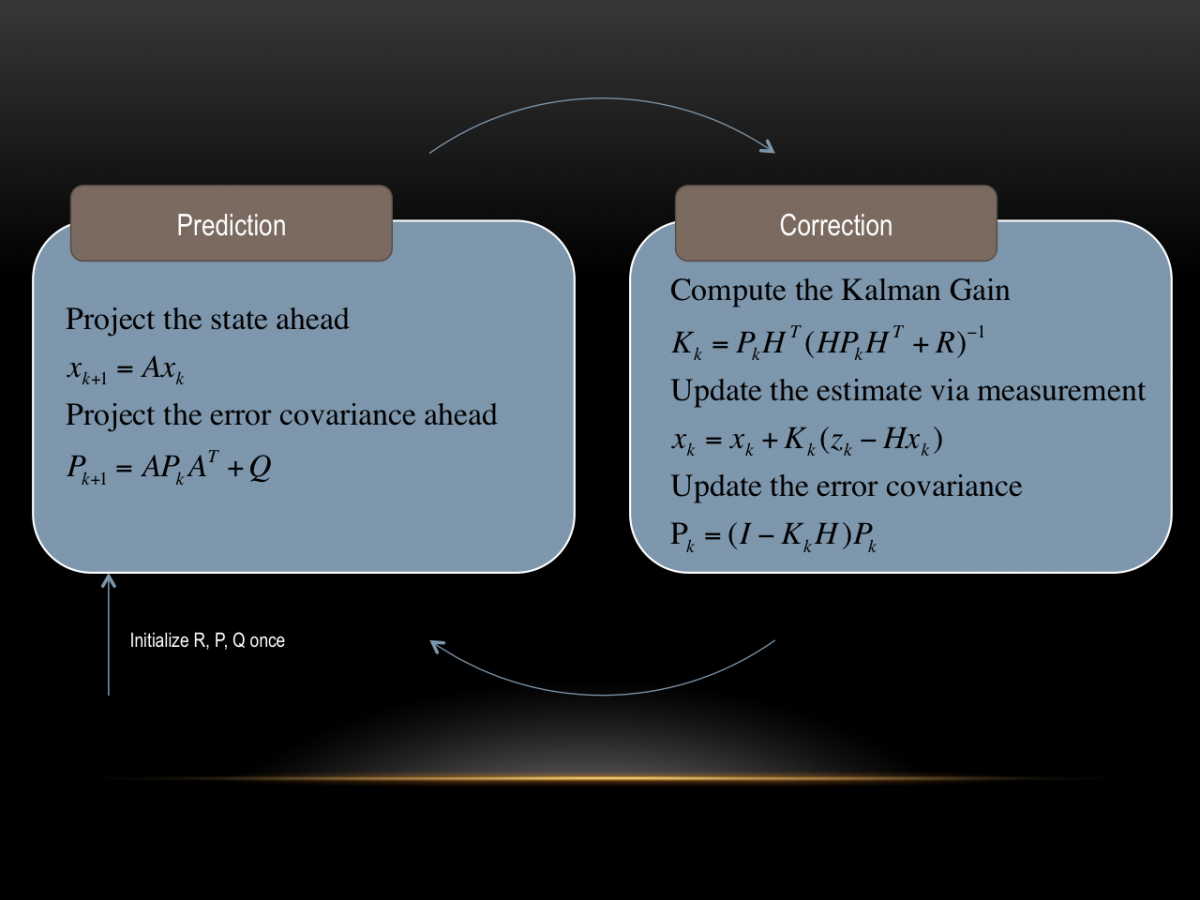
Herr Kalman hatte sich nun überlegt, wie man es schafft, trotz verrauschter Messung einzelner Sensoren, eine optimale Schätzung aller Zustände zu berechnen.