Fahrerassistenzsysteme entlasten den Fahrzeugführer und erhöhen den Fahrkomfort, das ist bekannt. Was aber vielleicht weniger bekannt ist, ist die Tatsache, dass mit den Systemen auch insgesamt für alle anderen Fahrzeuge/Verkehrsteilnehmer eine Verbesserung zu erreichen ist.
Die Ursache eines Stau ist selten ein Unfall o.ä., meist jedoch einfach eine zu stark befahrene Straße. Die PKW, die pro Stunde über den Streckenabschnitt fahren wollen, sind einfach zu viel für die Straße. Doch wie kann ein Fahrerassistenzsystem daran etwas ändern?
Verkehrsstromstärke und Verkehrsdichte
In der Verkehrstelematik wird mit der Verkehrsstromstärke die Anzahl der PKW die pro Stunde einen Abschnitt durchfahren, bezeichnet.
Die PKW, welche auf einen Kilometer Straße passen, werden als Verkehrsdichte bezeichnet.
Damit sind die zwei grundlegendsten Parameter für die Beschreibung der Verkehrssituation auf einer Straße schon erklärt.
Einfach Beispiel: In einem Stau stehen die Autos Stoßstange an Stoßstange, die Verkehrsdichte ist extrem hoch, die Verkehrsstromstärke aber 0. Bei freier Fahrt ist die Verkehrsstromstärke von der Fahrgeschwindigkeit abhängig, denn es ist ein Sicherheitsabstand einzuhalten.
Rechnet man z.B. die Fahrzeuglänge mit 4m, den Reserveabstand im Stau mit 1m und nimmt an, dass alle die Abstandsregel “1/2 Tacho” beachten, so ergibt sich folgende theoretische Verkehrsstromstärke in Abhängigkeit der Fahrzeuggeschwindigkeit.
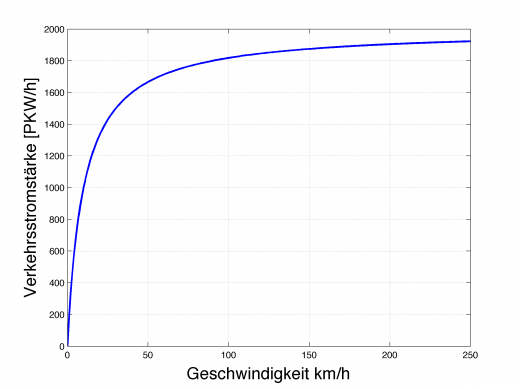
Theoretische Verkehrsstromstärke bei freier Fahrt und Abstand “1/2 Tacho”
Theorie vs. Realität
Leider funktioniert das in der Realität so nicht. Verschiedene reale Messungen [vgl. VTTI] auf Autobahnen haben ergeben, dass die Verkehrsstromstärke mit steigender Geschwindigkeit wieder abnimmt. Dieser Zusammenhang wurde von Herrn Greenshield bereits um 1935 herum festgestellt und empirisch ermittelt. Seither gilt das Greenshield Modell, welches den Zusammenhang zwischen Verkehrsdichte und Fahrgeschwindigkeit beschreibt.
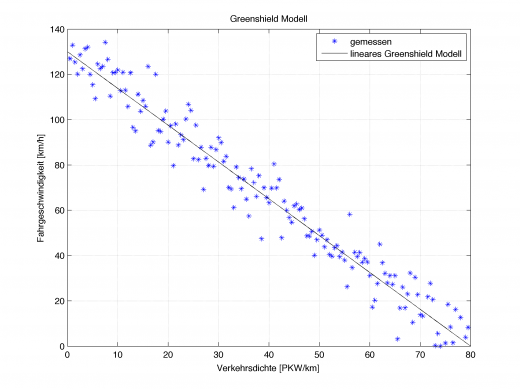
Lineares Greenshield Modell für freie Fahrgeschwindigkeit von 130km/h und maximaler Verkehrsdichte von 80PKW/km
Es besagt, dass man so lange seine Wunschgeschwindigkeit xf (hier: 130km/h) fahren kann, bis ein anderes Auto auf der Straße ist. Sobald mehr als xd=1 PKW/km auf der Straße unterwegs ist, muss ich irgendwie langsamer fahren. Die Messungen haben ergeben, dass man in 1. Näherung einen linearen Zusammenhang zwischen den beiden Größen aufstellen kann. Die maximale Verkehrsdichte xdmax ist straßenabhängig (Anzahl Spuren usw.).
Fundamentaldiagramm
Und jetzt kommt der Gag an der Sache! Wenn man diesen Zusammenhang, nämlich die Abhängigkeit der Fahrgeschwindigkeit (und somit der Anzahl PKW/h) von der Anzahl der PKW auf der Straße, mit der Verkehrsstromstärke multipliziert, so erhält man das Fundamentaldiagramm des Verkehrsflusses.
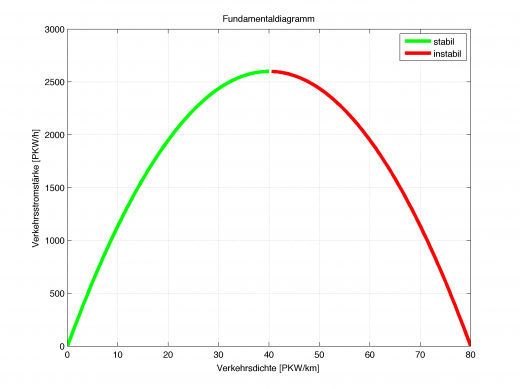
Auf Grund der linearen Annahme im Greenshield-Modell ergibt sich hier eine ideale Parabel, welche ihr Maximum bei halber maximaler Verkehrsdichte (hier 40PKW/km) hat. Interessant ist auch: Im roten Bereich der Parabel entsteht Stau! Die Stauwelle (auch Schockwelle genannt) hat eine negative Geschwindigkeit, welche genau dem Anstieg der Parabel entspricht und sich entgegen der Fahrtrichtung bewegt.
(schön ab 0:30min zu sehen)
Wie kann ein Assistenzsystem die Leistungsfähigkeit erhöhen?
Die Sache ist folgende: Die Realen Messungen sind natürlich mit realen Fahrzeugen entstanden, in denen Menschen saßen, die die Fahrzeuge gelenkt haben. Gehen wir von einer Reaktionszeit von 3s aus (was bei langweiliger Fahrt und rumspielen am Handy oder Radio durchaus üblich ist), welche der Fahrer benötigt um auf eine Reaktion vor ihm zu reagieren. Gehen wir weiterhin davon aus, dass er dann mit 0.3g verzögert, was einer etwas stärkeren Bremsung gleicht. Außerdem ist das Fahrzeug samt Reserveabstand zum Vordermann 4.5m lang. Dann legt das Fahrzeug folgende Wege zurück:
Die Berechnung des Bremswegs kommt aus der gleichmäßig verzögerten Abbremsung des Fahrzeugs und ist abhängig vom Reibwert zwischen Straße+Rad sowie von der Erdbeschleunigung. Dazu noch die Fahrzeuglänge und der Reserveabstand.
![Abstand zwischen zwei Fahrzeugen [Quelle: Script zur Vorlesung Verkehrstelematik, Prof. Krimmling, TU Dresden]](https://www.cbcity.de/wp-content/uploads/2013/07/Abstand-zwischen-PKW-520x287.png)
Abstand zwischen zwei Fahrzeugen [Quelle: Script zur Vorlesung Verkehrstelematik, Prof. Krimmling, TU Dresden]
Und durch Multiplikation mit der Verkehrsstromgeschwindigkeit die Verkehrsstromstärke in PKW/h.
Der entscheidende Fakt ist, dass sich das Fundamentaldiagramm mit steigender Reaktionszeit immer flacher drückt.
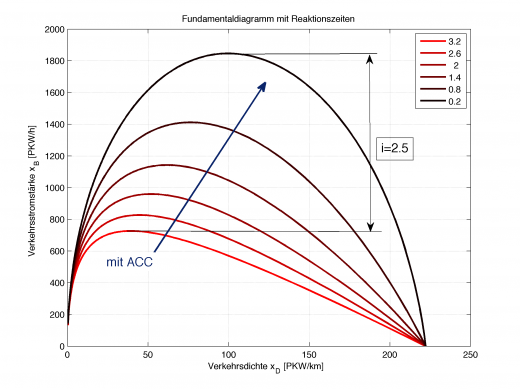
Das Fundamentaldiagramm für verschiedene Reaktionszeit (rot=lange Reaktionszeit, schwarz=ideal, unmöglich)
Wenngleich eine Reaktionszeit von 0s auch mit einer adaptiven Geschwindigkeitsregelanlage (ACC) nicht möglich ist, so sind doch Reaktionszeiten von 0.5s realisierbar. Im Vergleich zum menschlichen Fahrer, welcher eine Reaktionszeit von 3s hat, ist damit eine Erhöhung der Leistungsfähigkeit der Straße von:
für dieses Berechnungsbeispiel möglich. Auch für alle anderen Fahrer, welche das System nicht nutzen, denn sie profitieren ja von einer insgesamt ruhigeren Fahrweise.
Matlab Code zur Berechnung des Fundamentaldiagramms
%% Kapazitätserhöhung durch ACC
% Paul Balzer
% TU Dresden
clear all; close all; clc
for tau = 3.2:-0.6:0.2
%% Parameter
L = 3.5; % Fahrzeuglänge in m
Lr= 1.0; % Reserveabstand in m
v = 0:.1:140; % Fahrgeschwindigkeit
%tau=1.0; % Reaktionszeit in s
mu = 0.3; % Reibwert Straße
g = 9.81; % Erdbeschleunigung in m/s2
%% Wegberechnung
Lt = tau.*v;
Lb = v.^2./(2*mu*g);
ds = Lt+Lb+Lr+L;
%% Verkehrsdichte
xd=1./ds*1000; % in PKW/km
%% Verkehrsstromstärke
xb=xd.*v.*3.6; % in PKW/h
%% Fundamentaldiagramm
figure(1)
plot(xd,xb,'Linewidth',2,'color',[(0.99*tau)/3.2 0 0])
hold on
max(xb)
end
%% Abspeichern
legend(num2str((3.2:-0.6:0.2)'))
grid on
xlabel('Verkehrsdichte x_D [PKW/km]')
ylabel('Verkehrsstromstärke x_B [PKW/h]')
title(['Fundamentaldiagramm mit Reaktionszeiten'])
print(gcf,'-dpng','-r300',['Fundamentaldiagramm-Reaktionszeiten.png'])






One Comment