Das ist so schwer, das kann gar nicht verrutschen!

So oder so ähnlich hört man oft stolze Kraftfahrer tönen, wenn sie es geschafft haben mit Spanngurten o.ä. die Ladung auf der Ladefläche zu sichern. Ähnliches mit Ladung auf dem Hänger oder im Kofferraum. Als Beweis für alle Umstehenden und zur Beruhigung des eigenen Gewissens hält meißt der “ich rüttel am Gegenstand und kann ihn nicht verschieben”-Test her.

Doch hier liegt genau das Problem: Nur weil ein Transportgegenstand (z.B. Waschmaschine, Geschirrspüler, Palette Steine etc.) schwer ist und von Menschenhand nicht mehr leicht bewegt werden kann ist er noch lange nicht gut gesichert. Warum?

Wie gesagt, eine Palette Steine wiegt mal locker 815kg. Wird diese auf eine Ladefläche gestellt, so schafft es ein Mensch im Allgemeinen nicht mehr diese auch nur 1mm zu verschieben. Rückschluss: Steht bombensicher? Falsch.

Verrutschen einer ungesicherten Ladung

Am einfachen Beispiel der Kurvenfahrt soll dies mal verdeutlicht werden:

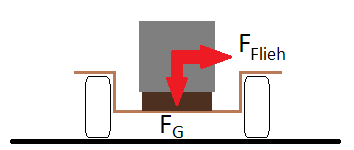
Die Steinpalette erzeugt eine Gewichtskraft von

$F_G=m \cdot g=815kg \cdot 9{,}81\cfrac{m}{s^2} \approx 8kN$

Beim Befahren einer Kurve entsteht eine Fliehkraft in Richtung des Kurvenäußeren, welche vom Kurvenradius R, der Fahrgeschwindigkeit v und der Masse m des Gegenstands abhängt.

$F_\text{Flieh}=m \cdot \cfrac{v^2}{R}$

Die Palette Steine fängt an zu rutschen, wenn die Fliehkraft größer wird als die hemmende Reibkraft, welche zwischen Aufstandsfläche und Ladung wirkt. Diese hemmende Reibkraft ist vor allem vom Reibwert µ und der Masse m abhängig.

Nimmt man jetzt an, dass zwischen der Palette Steine und der Ladefläche ein Reibwert von µ=0.20 wirkt, so ist die kritische Geschwindigkeit, ab welcher die Ladung beginnen würde zu rutschen, nachfolgend zu ermitteln:

$F_\text{Flieh} \ge \mu \cdot F_G$

$m \cdot \cfrac{v^2}{R} \ge \mu \cdot m \cdot g$

$v_\text{krit} \ge \sqrt{\mu \cdot g \cdot R}$

Fehler in der Formel? Die Masse ist garnicht mehr dabei. Nein, kein Fehler. Die Masse des zu transportierenden Gegenstandes hat keinen Einfluss auf die kritische Kurvengeschwindigkeit, ab welcher der Gegenstand anfangen würde auf der Ladefläche zu rutschen. Somit ist der Test, an der Steinpalette zu rütteln, um darauf zu schließen, dass sie fest steht, völlig irreführend!

$v_\text{krit} \ge \sqrt{0{,}2 \cdot 9{,}81\cfrac{m}{s^2} \cdot 100m}=14\cfrac{m}{s} \approx 50\cfrac{km}{h}$

Bei einem Kurvenradius von 100m und einem Reibwert von 0,2 ergibt sich also eine kritische Kurvengeschwindigkeit von 50km/h.

Diese kritische Kurvengeschwindigkeit kann nur dadurch gesteigert werden, dass entweder der Reibwert erhöht wird (z.B. mit Antirutschmatten) oder der Gegenstand mit Zurrgurten niedergehalten wird. Dadurch “erhöht” sich die auf die Ladefläche wirkende Gewichtskraft und somit auch die Reibkraft.

Verrutschen einer gesicherten Ladung

Wie soeben beschrieben, kann die kritische Kurvengeschwindigkeit erhöht werden, indem die Steinpalette durch Zurrgurte niedergehalten wird.

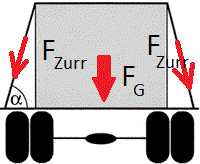
Die Gurte werden über die Ladung gelegt und fest gezurrt. Geht man von einem frei rutschenden Gurt über der Ladung aus, so ist diese Zurrkraft auf beiden Seiten identisch. Die Normalkraft, welche jetzt auf die Ladefläche wirkt, setzt sich zusammen aus Gewichtskraft und Niederhalterkraft.

$F_N=F_G+F_\text{Nieder}$

$F_N=m \cdot g + 2 \cdot F_\text{Zurr} \cdot \sin{(\alpha)}$

Die kritische Kurvengeschwindigkeit kann jetzt durch Vorspannen der Zurrgurte und unterlegen einer Antirutschmatte erhöht werden.

$m \cdot \cfrac{v^2}{R} \ge \mu \cdot (m \cdot g + 2 \cdot F_\text{Zurr} \cdot \sin{(\alpha)})$

$v_\text{Krit} \ge \sqrt{\mu g R + \cfrac{2 \mu R}{m} \cdot F_\text{Zurr} \cdot \sin{(\alpha)})}$

Setzt man dort z.B. typische 3500N Spannkraft ein, ergibt sich z.B. folgende kritische Kurvengeschwindigkeit:

$v_\text{Krit} \ge \sqrt{0{,}2 \cdot 9{,}81 \cfrac{m}{s^2} \cdot 100m + \cfrac{2 \cdot 0{,}2 \cdot 100m}{815kg} \cdot 3500N \cdot \sin(80^\circ)}$

$v_\text{Krit} \ge \sqrt{196\cfrac{m^2}{s^2}+169\cfrac{m^2}{s^2}}=19{,}1\cfrac{m}{s} \approx 69\cfrac{km}{h}$

Die Kurvengeschwindigkeit bei der die Ladung gerade nicht mehr verrutscht, kann durch Niederzurren oder äquivalent eine Antirutschmatte gesteigert werden.

Vollbremsung

Wird das Fahrzeug gebremst, so entstehen typische Verzögerungen von

$a_x = -10\cfrac{m}{s^2}$

Newtons Axiome helfen um auf die entstehende Kraft zu schließen. Die Ladung würde nach vorn rutschen, sobald die Verzögerungskraft größer als die wirkende Reibkraft ist.

$m \cdot a_x \ge \mu m g$

$a_\text{Krit} \ge \mu \cdot g$

Auch diese kritische Situation ist nicht von der Masse des zu transportierenden Gegenstandes abhängig sondern ausschließlich vom Reibwert zwischen Ladefläche und Gegenstand. Werte von µ=0,2 lassen die kritische Verzögerung auf

$a_\text{Krit} \ge 0{,}2 \cdot 9{,}81 \cfrac{m}{s^2} \approx 2\cfrac{m}{s^2}$

sinken. Das ist wirklich viel zu wenig! Daher sollte Ladung immer nach folgender Anleitung gesichert werden:

Hinweise zur Ladungssicherung

Video dazu:

Motorblog